author: zlotus

Description:

這是MIT 18.06 Linear-Algebra 的學習筆記

Course video

第三十一講：線性變換及對應矩陣

如何判斷一個操作是不是線性變換？線性變換需滿足以下兩個要求：

即變換\(T\)需要同時滿足加法和數乘不變的性質。將兩個性質合成一個式子為：\(T(cv+dw)=cT(v)+dT(w)\)

例1，二維空間中的投影操作，\(T: \mathbb{R}^2\to\mathbb{R}^2\)，它可以將某向量投影在一條特定直線上。檢查一下投影操作，如果我們將向量長度翻倍，則其投影也翻倍；兩向量相加後做投影與兩向量做投影再相加結果一致。所以投影操作是線性變換。

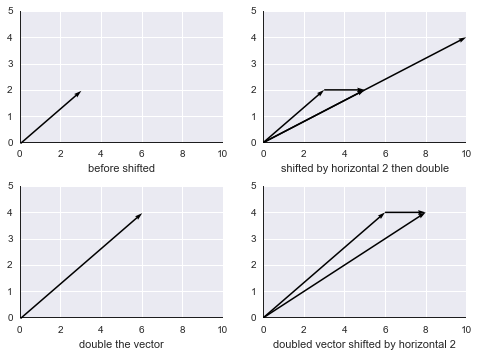
“壞”例1，二維空間的平移操作，即平面平移：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np


fig = plt.figure()

sp1 = plt.subplot(221)
vectors_1 = np.array([[0,0,3,2],]) 
X_1, Y_1, U_1, V_1 = zip(*vectors_1)
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
sp1.quiver(X_1, Y_1, U_1, V_1, angles='xy', scale_units='xy', scale=1)
sp1.set_xlim(0, 10)
sp1.set_ylim(0, 5)
sp1.set_xlabel("before shifted")

sp2 = plt.subplot(222)
vector_2 = np.array([[0,0,3,2],
                     [3,2,2,0],
                     [0,0,5,2],
                     [0,0,10,4]]) 
X_2,Y_2,U_2,V_2 = zip(*vector_2)
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
sp2.quiver(X_2, Y_2, U_2, V_2, angles='xy', scale_units='xy', scale=1)
sp2.set_xlim(0, 10)
sp2.set_ylim(0, 5)
sp2.set_xlabel("shifted by horizontal 2 then double")

sp3 = plt.subplot(223)
vectors_1 = np.array([[0,0,6,4],]) 
X_1, Y_1, U_1, V_1 = zip(*vectors_1)
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
sp3.quiver(X_1, Y_1, U_1, V_1, angles='xy', scale_units='xy', scale=1)
sp3.set_xlim(0, 10)
sp3.set_ylim(0, 5)
sp3.set_xlabel("double the vector")

sp4 = plt.subplot(224)
vector_2 = np.array([[0,0,6,4],
                     [6,4,2,0],
                     [0,0,8,4]]) 
X_2,Y_2,U_2,V_2 = zip(*vector_2)
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
sp4.quiver(X_2, Y_2, U_2, V_2, angles='xy', scale_units='xy', scale=1)
sp4.set_xlim(0, 10)
sp4.set_ylim(0, 5)
sp4.set_xlabel("doubled vector shifted by horizontal 2")

plt.subplots_adjust(hspace=0.33)
plt.draw()

plt.close(fig)

比如，上圖中向量長度翻倍，再做平移，明顯與向量平移後再翻倍的結果不一致。

有時我們也可以用一個簡單的特例判斷線性變換，檢查\(T(0)\stackrel{?}{=}0\)。零向量平移後結果並不為零。

所以平面平移操作並不是線性變換。

“壞”例2，求模運算，\(T(v)=\|v\|,\ T:\mathbb{R}^3\to\mathbb{R}^1\)，這顯然不是線性變換，比如如果我們將向量翻倍則其模翻倍，但如果我將向量翻倍取負，則其模依然翻倍。所以\(T(-v)\neq -T(v)\)

例2，旋轉\(45^\circ\)操作，\(T:\mathbb{R}^2\to\mathbb{R}^2\)，也就是將平面內一個向量映射為平面內另一個向量。檢查可知，如果向量翻倍，則旋轉後同樣翻倍；兩個向量先旋轉後相加，與這兩個向量先相加後旋轉得到的結果一樣。

所以從上面的例子我們知道，投影與旋轉都是線性變換。

例3，矩陣乘以向量，\(T(v)=Av\)，這也是一個（一系列）線性變換，不同的矩陣代表不同的線性變換。根據矩陣的運算法則有\(A(v+w)=A(v)+A(w),\ A(cv)=cAv\)。比如取\(A=\begin{bmatrix}1&0\\0&-1\end{bmatrix}\)，作用於平面上的向量\(v\)，會導致\(v\)的\(x\)分量不變，而\(y\)分量取反，也就是圖像沿\(x\)軸翻轉。

線性變換的核心，就是該變換使用的相應的矩陣。

比如我們需要做一個線性變換，將一個三維向量降至二維，\(T:\mathbb{R}^3\to\mathbb{R}^2\)，則在\(T(v)=Av\)中，\(v\in\mathbb{R}^3,\ T(v)\in\mathbb{R}^2\)，所以\(A\)應當是一個\(2\times 3\)矩陣。

如果我們希望知道線性變換\(T\)對整個輸入空間\(\mathbb{R}^n\)的影響，我們可以找到空間的一組基\(v_1,\ v_2,\ \cdots,\ v_n\)，檢查\(T\)對每一個基的影響\(T(v_1),\ T(v_2),\ \cdots,\ T(v_n)\)，由於輸入空間中的任意向量都滿足：

所以我們可以根據\(T(v)\)推出線性變換\(T\)對空間內任意向量的影響，得到：

現在我們需要考慮，如何把一個與坐標無關的線性變換變成一個與坐標有關的矩陣呢？

在\(1\)式中，\(c_1,c_2,\cdots,c_n\)就是向量\(v\)在基\(v_1,v_2,\cdots,v_n\)上的坐標，比如分解向量\(v=\begin{bmatrix}3\\2\\4\end{bmatrix}=3\begin{bmatrix}1\\0\\0\end{bmatrix}+2\begin{bmatrix}0\\1\\0\end{bmatrix}+4\begin{bmatrix}0\\0\\1\end{bmatrix}\)，式子將向量\(v\)分解在一組標準正交基\(\begin{bmatrix}1\\0\\0\end{bmatrix},\begin{bmatrix}0\\1\\0\end{bmatrix},\begin{bmatrix}0\\0\\1\end{bmatrix}\)上。當然，我們也可以選用矩陣的特征向量作為基向量，基的選擇是多種多樣的。

我們打算構造一個矩陣\(A\)用以表示線性變換\(T:\mathbb{R}^n\to\mathbb{R}^m\)。我們需要兩組基，一組用以表示輸入向量，一組用以表示輸出向量。令\(v_1,v_2,\cdots,v_n\)為輸入向量的基，這些向量來自\(\mathbb{R}^n\)；\(w_1,w_2,\cdots,w_m\)作為輸出向量的基，這些向量來自\(\mathbb{R}^m\)。

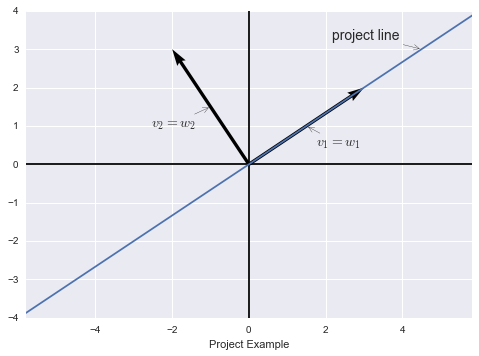
我們用二維空間的投影矩陣作為例子：

fig = plt.figure()

vectors_1 = np.array([[0, 0, 3, 2],
                      [0, 0, -2, 3]]) 
X_1, Y_1, U_1, V_1 = zip(*vectors_1)
plt.axis('equal')
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
plt.quiver(X_1, Y_1, U_1, V_1, angles='xy', scale_units='xy', scale=1)
plt.plot([-6, 12], [-4, 8])
plt.annotate('$$v_1=w_1$$', xy=(1.5, 1), xytext=(10, -20), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.annotate('$$v_2=w_2$$', xy=(-1, 1.5), xytext=(-60, -20), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.annotate('project line', xy=(4.5, 3), xytext=(-90, 10), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))

ax = plt.gca()
ax.set_xlim(-5, 5)
ax.set_ylim(-4, 4)
ax.set_xlabel("Project Example")

plt.draw()

plt.close(fig)

從圖中可以看到，設輸入向量的基為\(v_1,v_2\)，\(v_1\)就在投影上，而\(v_2\)垂直於投影方向，輸出向量的基為\(w_1,w_2\)，而\(v_1=w_1,v_2=w_2\)。那麽如果輸入向量為\(v=c_1v_1+c_2v_2\)，則輸出向量為\(T(v)=c_1v_1\)，也就是線性變換去掉了法線方向的分量，輸入坐標為\((c_1,c_2)\)，輸出坐標變為\((c_1,0)\)。

找出這個矩陣並不困難，\(Av=w\)，則有\(\begin{bmatrix}1&0\\0&0\end{bmatrix}\begin{bmatrix}c_1\\c_2\end{bmatrix}=\begin{bmatrix}c_1\\0\end{bmatrix}\)。

本例中我們選取的基極為特殊，一個沿投影方向，另一個沿投影法線方向，其實這兩個向量都是投影矩陣的特征向量，所以我們得到的線性變換矩陣是一個對角矩陣，這是一組很好的基。

所以，如果我們選取投影矩陣的特征向量作為基，則得到的線性變換矩陣將是一個包含投影矩陣特征值的對角矩陣。

繼續這個例子，我們不再選取特征向量作為基，而使用標準基\(v_1=\begin{bmatrix}1\\0\end{bmatrix},v_2=\begin{bmatrix}0\\1\end{bmatrix}\)，我們繼續使用相同的基作為輸出空間的基，即\(v_1=w_1,v_2=w_2\)。此時投影矩陣為\(P=\frac{aa^T}{a^Ta}=\begin{bmatrix}\frac{1}{2}&\frac{1}{2}\\\frac{1}{2}&\frac{1}{2}\end{bmatrix}\)，這個矩陣明顯沒有上一個矩陣“好”，不過這個矩陣也是一個不錯的對稱矩陣。

總結通用的計算線性變換矩陣\(A\)的方法：

• 確定輸入空間的基\(v_1,v_2,\cdots,v_n\)，確定輸出空間的基\(w_1,w_2,\cdots,w_m\)；
• 計算\(T(v_1)=a_{11}w_1+a_{21}w_2+\cdots+a_{m1}w_m\)，求出的系數\(a_{i1}\)就是矩陣\(A\)的第一行；
• 繼續計算\(T(v_2)=a_{12}w_1+a_{22}w_2+\cdots+a_{m2}w_m\)，求出的系數\(a_{i2}\)就是矩陣\(A\)的第二行；
• 以此類推計算剩余向量直到\(v_n\)；
• 最終得到矩陣\(A=\left[\begin{array}{c\|c\|c\|c}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\\\end{array}\right]\)。

最後我們介紹一種不一樣的線性變換，\(T=\frac{\mathrm{d}}{\mathrm{d}x}\)：

• 設輸入為\(c_1+c_2x+c_3x^3\)，基為\(1,x,x^2\)；

• 則輸出為導數：\(c_2+2c_3x\)，基為\(1,x\)；

  所以我們需要求一個從三維輸入空間到二維輸出空間的線性變換，目的是求導。求導運算其實是線性變換，因此我們只要知道少量函數的求導法則（如\(\sin x, \cos x, e^x\)），就能求出它們的線性組合的導數。

  有\(A\begin{bmatrix}c_1\\c_2\\c_3\end{bmatrix}=\begin{bmatrix}c_2\\2c_3\end{bmatrix}\)，從輸入輸出的空間維數可知，\(A\)是一個\(2\times 3\)矩陣，\(A=\begin{bmatrix}0&1&0\\0&0&2\end{bmatrix}\)。

最後，矩陣的逆相當於對應線性變換的逆運算，矩陣的乘積相當於線性變換的乘積，實際上矩陣乘法也源於線性變換。