author: zlotus

Description:

這是MIT 18.06 Linear-Algebra 的學習筆記

Course video

第十二講：圖和網絡

圖和網絡

import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline

dg = nx.DiGraph()
dg.add_edges_from([(1,2), (2,3), (1,3), (1,4), (3,4)])
edge_labels = {(1, 2): 1, (1, 3): 3, (1, 4): 4, (2, 3): 2, (3, 4): 5}

pos = nx.spring_layout(dg)
nx.draw_networkx_edge_labels(dg,pos,edge_labels=edge_labels, font_size=16)
nx.draw_networkx_labels(dg, pos, font_size=20, font_color='w')
nx.draw(dg, pos, node_size=1500, node_color="gray")

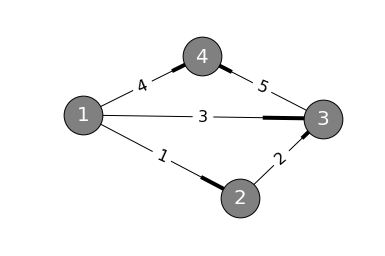
該圖由4個節點與5條邊組成，

我們可以建立$5 \times 4$矩陣 \(A= \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \\ \end{bmatrix}\)

觀察前三行，易看出這三個列向量線性相關，也就是這三個向量可以形成回路（loop）。

現在，解$Ax=0$： \(Ax= \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \\ \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\x_4\\ \end{bmatrix}\)。

展開得到： \(\begin{bmatrix}x_2-x_1 \\x_3-x_2 \\x_3-x_1 \\x_4-x_1 \\x_4-x_3 \\ \end{bmatrix}=\begin{bmatrix}0\\0\\0\\0\\0\\ \end{bmatrix}\)

引入矩陣的實際意義：將$x=\begin{bmatrix}x_1 & x_2 & x_3 & x_4\end{bmatrix}$設為各節點電勢（Potential at the Nodes）。

則式子中的諸如$x_2-x_1$的元素，可以看做該邊上的電勢差（Potential Differences）。

容易看出其中一個解\(x=\begin{bmatrix}1\\1\\1\\1\end{bmatrix}\)，即等電勢情況，此時電勢差為$0$。

化簡$A$易得$rank(A)=3$，所以其零空間維數應為$n-r=4-3=1$，即\(\begin{bmatrix}1\\1\\1\\1\end{bmatrix}\)就是其零空間的一組基。

其零空間的物理意義為，當電位相等時，不存在電勢差，圖中無電流。

當我們把圖中節點$4$接地後，節點$4$上的電勢為$0$，此時的 \(A= \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 0 \\ 0 & 0 & -1 \\ \end{bmatrix}\)，各列線性無關，$rank(A)=3$。

現在看看$A^Ty=0$（這是應用數學里最常用的式子）：

\(A^Ty=0=\begin{bmatrix}-1 & 0 & -1 & -1 & 0 \\1 & -1 & 0 & 0 & 0 \\0 & 1 & 1 & 0 & -1 \\0 & 0 & 0 & 1 & 1 \\ \end{bmatrix}\begin{bmatrix}y_1\\y_2\\y_3\\y_4\\y_5\end{bmatrix}=\begin{bmatrix}0\\0\\0\\0\end{bmatrix}\)，對於轉置矩陣有$dim N(A^T)=m-r=5-3=2$。

接著說上文提到的的電勢差，矩陣$C$將電勢差與電流聯系起來，電流與電勢差的關系服從歐姆定律：邊上的電流值是電勢差的倍數，這個倍數就是邊的電導（conductance）即電阻（resistance）的倒數。

$ 電勢差 \xrightarrow[歐姆定律]{矩陣C} 各邊上的電流y_1, y_2, y_3, y_4, y_5 $，而$A^Ty=0$的另一個名字叫做“克希荷夫電流定律”（Kirchoff’s Law, 簡稱KCL）。

再把圖拿下來觀察：

import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline

dg = nx.DiGraph()
dg.add_edges_from([(1,2), (2,3), (1,3), (1,4), (3,4)])
edge_labels = {(1, 2): 1, (1, 3): 3, (1, 4): 4, (2, 3): 2, (3, 4): 5}

pos = nx.spring_layout(dg)
nx.draw_networkx_edge_labels(dg,pos,edge_labels=edge_labels, font_size=16)
nx.draw_networkx_labels(dg, pos, font_size=20, font_color='w')
nx.draw(dg, pos, node_size=1500, node_color="gray")

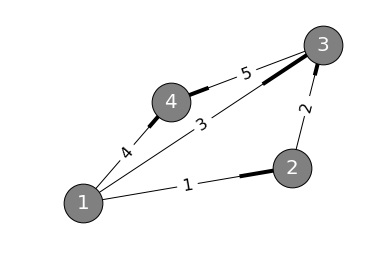
將$A^Ty=0$中的方程列出來： \(\left\{ \begin{aligned} y_1 + y_3 + y_4 &= 0 \\ y_1 - y_2 &= 0 \\ y_2 + y_3 - y_5 &= 0 \\ y_4 - y_5 &= 0 \\ \end{aligned} \right.\)

對比看$A^Ty=0$的第一個方程，$-y_1-y_3-y_4=0$，可以看出這個方程是關於節點$1$上的電流的，方程指出節點$1$上的電流和為零，克希荷夫定律是一個平衡方程、守恒定律，它說明了流入等於流出，電荷不會在節點上累積。

對於$A^T$，有上文得出其零空間的維數是$2$，則零空間的基應該有兩個向量。

• 現在假設$y_1=1$，也就是令$1$安培的電流在邊$1$上流動；
• 由圖看出$y_2$也應該為$1$；
• 再令$y_3=-1$，也就是讓$1$安培的電流流回節點$1$；
• 令$y_4=y_5=0$；

得到一個符合KCL的向量\(\begin{bmatrix}1\\1\\-1\\0\\0\end{bmatrix}\)，代回方程組发現此向量即為一個解，這個解发生在節點$1,2,3$組成的回路中，該解即為零空間的一個基。

根據上一個基的經驗，可以利用$1,3,4$組成的節點求另一個基：

• 令$y_1=y_2=0$；
• 令$y_3=1$；
• 由圖得$y_5=1$；
• 令$y_4=-1$；

得到令一個符合KCL的向量\(\begin{bmatrix}0\\0\\1\\-1\\1\end{bmatrix}\)，代回方程可知此為另一個解。

則$N(A^T)$的一組基為\(\begin{bmatrix}1\\1\\-1\\0\\0\end{bmatrix}\quad\begin{bmatrix}0\\0\\1\\-1\\1\end{bmatrix}\)。

看圖，利用節點$1,2,3,4$組成的大回路（即邊$1,2,5,4$）：

• 令$y_3=0$；
• 令$y_1=1$；
• 則由圖得$y_2=1, y_5=1, y_4=-1$；

得到符合KCL的向量\(\begin{bmatrix}1\\1\\0\\-1\\1\end{bmatrix}\)，易看出此向量為求得的兩個基之和。

接下來觀察$A$的列空間，即$A^T$的行空間，方便起見我們直接計算 \(A^T= \begin{bmatrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \\ \end{bmatrix}\) 的行空間。

易從基的第一個向量看出前三行$A^T$的線性相關，則$A^T$的主行為第$1,2,4$行，對應在圖中就是邊$1,2,4$，可以发現這三條邊沒有組成回路，則在這里可以說線性無關等價於沒有回路。由$4$個節點與$3$條邊組成的圖沒有回路，就表明$A^T$的對應行向量線性無關，也就是節點數減一（$rank=nodes-1$）條邊線性無關。另外，沒有回路的圖也叫作樹（Tree）。

再看左零空間的維數公式：$dim N(A^T)=m-r$，左零空間的維數就是相互無關的回路的數量，於是得到$loops=edges-(nodes-1)$，整理得：

此等式對任何圖均有效，任何圖都有此拓撲性質，這就是著名的歐拉公式（Euler’s Formula）。$零維（節點）-一維（邊）+二維（回路）=1$便於記憶。

總結：

• 將電勢記為$e$，則在引入電勢的第一步中，有$e=Ax$；
• 電勢差導致電流產生，$y=Ce$；
• 電流滿足克希荷夫定律方程，$A^Ty=0$；

這些是在無電源情況下的方程。

電源可以通過：在邊上加電池（電壓源），或在節點上加外部電流 兩種方式接入。

如果在邊上加電池，會體現在$e=Ax$中；如果在節點上加電流，會體現在$A^Ty=f$中，$f$向量就是外部電流。

將以上三個等式連起來得到$A^TCAx=f$。另外，最後一個方程是一個平衡方程，還需要注意的是，方程僅描述平衡狀態，方程並不考慮時間。最後，$A^TA$是一個對稱矩陣。