author: zlotus

Description:

這是MIT 18.06 Linear-Algebra 的學習筆記

Course video

第一講：方程組的幾何解釋

我們從求解線性方程組來開始這門課，從一個普通的例子講起：方程組有$2$個未知數，一共有$2$個方程，分別來看方程組的“行圖像”和“列圖像”。

有方程组$\begin{cases}2x&-y&=0\\-x&+2y&=3\end{cases}$，寫作矩陣形式有$\begin{bmatrix}2&-1\\-1&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$，通常我們把第一個矩陣稱為係數矩陣$A$，將第二個矩陣稱為向量$x$，將第三個矩陣稱為向量$b$，於是線性方程組可以表示為$Ax=b$。

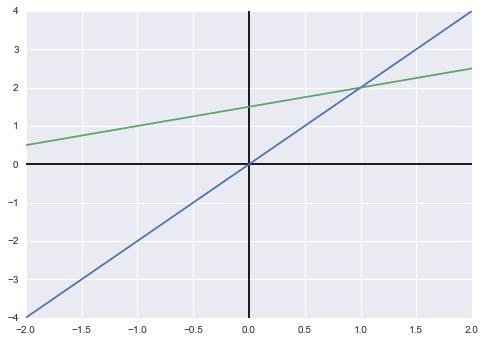
我們來看列圖像，即直角坐標系中的圖像：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

x = [-2, 2, -2, 2]
y = [-4, 4, 0.5, 2.5]

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')

plt.plot(x[:2], y[:2], x[2:], y[2:])

plt.draw()

plt.close(fig)

上圖是我們都很熟悉的直角坐標系中兩直線相交的情況，接下來我們按行觀察方程組 $x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$（我們把第一個向量稱作$col_1$，第二個向量稱作$col_2$，以表示第一行向量和第二行向量），要使得式子成立，需要第一個向量加上兩倍的第二個向量，即$1\begin{bmatrix}2\\-1\end{bmatrix}+2\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$。

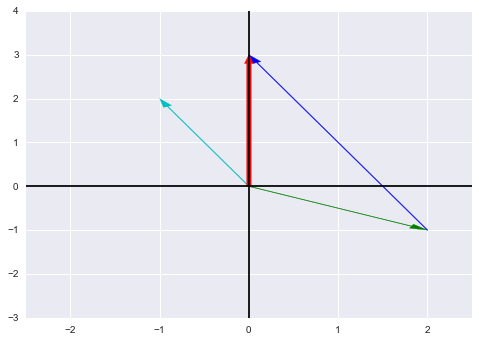
現在來看行圖像，在二維平面上畫出上面的行向量：

from functools import partial

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
ax = plt.gca()
ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-3, 4)

arrow_vector = partial(plt.arrow, width=0.01, head_width=0.1, head_length=0.2, length_includes_head=True)

arrow_vector(0, 0, 2, -1, color='g')
arrow_vector(0, 0, -1, 2, color='c')
arrow_vector(2, -1, -2, 4, color='b')
arrow_vector(0, 0, 0, 3, width=0.05, color='r')

plt.draw()

plt.close(fig)

如圖，綠向量$col_1$與藍向量（兩倍的藍綠向量$col_2$）合成紅向量$b$。

接著，我們繼續觀察 $x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$，$col_1,col_2$的某種線性組合得到了向量$b$，那麼$col_1,col_2$的所有線性組合能夠得到什麼結果？它們將鋪滿整個平面。

下面進入三個未知數的方程組：$\begin{cases}2x&-y&&=0\\-x&+2y&-z&=-1\\&-3y&+4z&=4\end{cases}$，寫作矩陣形式$A=\begin{bmatrix}2&-1&0\\-1&2&-1\\0&-3&4\end{bmatrix},\ b=\begin{bmatrix}0\\-1\\4\end{bmatrix}$。

在三維直角坐標系中，每一個方程將確定一個平面，而例子中的三個平面會相交於一點，這個點就是方程組的解。

同樣的，將方程組寫成行向量的線性組合，觀察行圖像：$x\begin{bmatrix}2\\-1\\0\end{bmatrix}+y\begin{bmatrix}-1\\2\\-3\end{bmatrix}+z\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}$。易知教授特意安排的例子中最後一個行向量恰巧等於等式右邊的$b$向量，所以我們需要的線性組合為$x=0,y=0,z=1$。假設我們令$b=\begin{bmatrix}1\\1\\-3\end{bmatrix}$，則需要的線性組合為$x=1,y=1,z=0$。

我們並不能總是這麼輕易的求出正確的線性組合，所以下一講將介紹消元法——一種線性方程組的系統性解法。

現在，我們需要考慮，對於任意的$b$，是否都能求解$Ax=b$？用行向量線性組合的觀點闡述就是，行向量的線性組合能否覆蓋整個三維向量空間？對上面這個例子，答案是肯定的，這個例子中的$A$是我們喜歡的矩陣類型，但是對另一些矩陣，答案是否定的。那麼在什麼情況下，三個向量的線性組合得不到$b$？

——如果三個向量在同一個平面上，問題就出現了——那麼他們的線性組合也一定都在這個平面上。舉個例子，比如$col_3=col_1+col_2$，那麼不管怎麼組合，這三個向量的結果都逃不出這個平面，因此當$b$在平面內，方程組有解，而當$b$不在平面內，這三個列向量就無法構造出$b$。在後面的課程中，我們會了解到這種情形稱為奇異、矩陣不可逆。

下面我們推廣到九維空間，每個方程有九個未知數，共九個方程，此時已經無法從坐標圖像中描述問題了，但是我們依然可以從求九維行向量線性組合的角度解決問題，仍然是上面的問題，是否總能得到$b$？當然這仍取決於這九個向量，如果我們取一些並不相互獨立的向量，則答案是否定的，比如取了九行但其實只相當於八行，有一行毫無貢獻（這一行是前面行的某種線性組合），則會有一部分$b$無法求得。

接下來介紹方程的矩陣形式$Ax=b$，這是一種乘法運算，舉個例子，取$A=\begin{bmatrix}2&5\\1&3\end{bmatrix},\ x=\begin{bmatrix}1\\2\end{bmatrix}$，來看如何計算矩陣乘以向量：

• 我們依然使用列向量線性組合的方式，一次計算一行，$\begin{bmatrix}2&5\\1&3\end{bmatrix}\begin{bmatrix}1\\2\end{bmatrix}=1\begin{bmatrix}2\\1\end{bmatrix}+2\begin{bmatrix}5\\3\end{bmatrix}=\begin{bmatrix}12\\7\end{bmatrix}$
• 另一種方法，使用向量內積，矩陣第一列向量點乘$x$向量$\begin{bmatrix}2&5\end{bmatrix}\cdot\begin{bmatrix}1&2\end{bmatrix}^T=12,\ \begin{bmatrix}1&3\end{bmatrix}\cdot\begin{bmatrix}1&2\end{bmatrix}^T=7$。

教授建議使用第一種方法，將$Ax$看做$A$行向量的線性組合。