深度學習500問-02-機器學習基礎
03 Feb 2021 | deep learningauthor: scutan90
Description:
深度學習內容相關筆記
第二章 機器學習基礎
機器學習起源於上世紀50年代,1959年在IBM工作的Arthur Samuel設計了一個下棋程序,這個程序具有學習的能力,它可以在不斷的對弈中提高自己。由此提出了“機器學習”這個概念,它是一個結合了多個學科如概率論,優化理論,統計等,最終在計算機上實現自我獲取新知識,學習改善自己的這樣一個研究領域。機器學習是人工智能的一個子集,目前已經发展出許多有用的方法,比如支持向量機,回歸,決策樹,隨機森林,強化方法,集成學習,深度學習等等,一定程度上可以幫助人們完成一些數據預測,自動化,自動決策,最優化等初步替代腦力的任務。本章我們主要介紹下機器學習的基本概念、監督學習、分類算法、邏輯回歸、代價函數、損失函數、LDA、PCA、決策樹、支持向量機、EM算法、聚類和降維以及模型評估有哪些方法、指標等等。
2.1 基本概念
2.1.1 大話理解機器學習本質
機器學習(Machine Learning, ML),顧名思義,讓機器去學習。這里,機器指的是計算機,是算法運行的物理載體,你也可以把各種算法本身當做一個有輸入和輸出的機器。那麽到底讓計算機去學習什麽呢?對於一個任務及其表現的度量方法,設計一種算法,讓算法能夠提取中數據所蘊含的規律,這就叫機器學習。如果輸入機器的數據是帶有標簽的,就稱作有監督學習。如果數據是無標簽的,就是無監督學習。
2.1.2 什麽是神經網絡
神經網絡就是按照一定規則將多個神經元連接起來的網絡。不同的神經網絡,具有不同的連接規則。例如全連接(Full Connected, FC)神經網絡,它的規則包括:
(1)有三種層:輸入層,輸出層,隱藏層。
(2)同一層的神經元之間沒有連接。
(3)fully connected的含義:第 N 層的每個神經元和第 N-1 層的所有神經元相連,第 N-1 層神經元的輸出就是第 N 層神經元的輸入。
(4)每個連接都有一個權值。
神經網絡架構
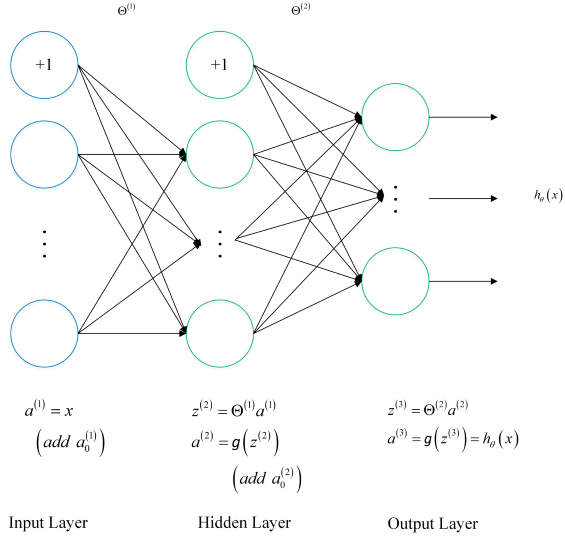
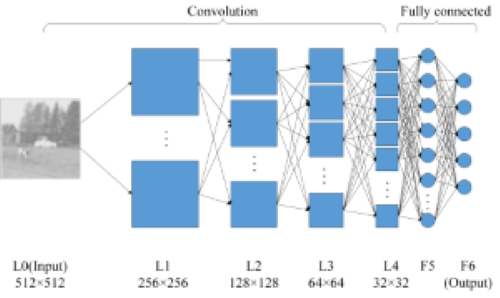
圖2-1就是一個神經網絡系統,它由很多層組成。輸入層負責接收信息,比如一只貓的圖片。輸出層是計算機對這個輸入信息的判斷結果,它是不是貓。隱藏層就是對輸入信息的傳遞和加工處理。

圖2-1 神經網絡系統
2.1.3 各種常見算法圖示
日常使用機器學習的任務中,我們經常會遇見各種算法,圖2-2是各種常見算法的圖示。
| 回歸算法 | 聚類算法 | 正則化方法 |
|---|---|---|
 |
 |
 |
| 決策樹學習 | 貝葉斯方法 | 基於核的算法 |
|---|---|---|
 |
 |
 |
| 聚類算法 | 關聯規則學習 | 人工神經網絡 |
|---|---|---|
 |
 |
 |
| 深度學習 | 降低維度算法 | 集成算法 |
|---|---|---|
 |
 |
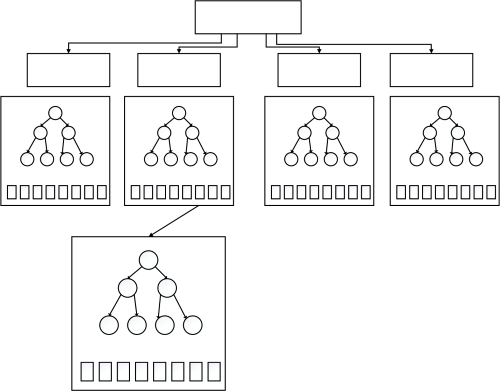 |
圖2-2 各種常見算法圖示
2.1.4 計算圖的導數計算
計算圖導數計算是反向傳播,利用鏈式法則和隱式函數求導。
假設 $z = f(u,v)$ 在點 $(u,v)$ 處偏導連續,$(u,v)$是關於 $t$ 的函數,在 $t$ 點可導,求 $z$ 在 $t$ 點的導數。
根據鏈式法則有
\(\frac{dz}{dt}=\frac{\partial z}{\partial u}.\frac{du}{dt}+\frac{\partial z}{\partial v}
.\frac{dv}{dt}\)
鏈式法則用文字描述:“由兩個函數湊起來的覆合函數,其導數等於里邊函數代入外邊函數的值之導數,乘以里邊函數的導數。
為了便於理解,下面舉例說明:
\(f(x)=x^2,g(x)=2x+1\)
則:
\({f[g(x)]}'=2[g(x)] \times g'(x)=2[2x+1] \times 2=8x+4\)
2.1.5 理解局部最優與全局最優
笑談局部最優和全局最優
柏拉圖有一天問老師蘇格拉底什麽是愛情?蘇格拉底叫他到麥田走一次,摘一顆最大的麥穗回來,不許回頭,只可摘一次。柏拉圖空著手出來了,他的理由是,看見不錯的,卻不知道是不是最好的,一次次僥幸,走到盡頭時,才发現還不如前面的,於是放棄。蘇格拉底告訴他:“這就是愛情。”這故事讓我們明白了一個道理,因為生命的一些不確定性,所以全局最優解是很難尋找到的,或者說根本就不存在,我們應該設置一些限定條件,然後在這個範圍內尋找最優解,也就是局部最優解——有所斬獲總比空手而歸強,哪怕這種斬獲只是一次有趣的經歷。 柏拉圖有一天又問什麽是婚姻?蘇格拉底叫他到樹林走一次,選一棵最好的樹做聖誕樹,也是不許回頭,只許選一次。這次他一身疲憊地拖了一棵看起來直挺、翠綠,卻有點稀疏的杉樹回來,他的理由是,有了上回的教訓,好不容易看見一棵看似不錯的,又发現時間、體力已經快不夠用了,也不管是不是最好的,就拿回來了。蘇格拉底告訴他:“這就是婚姻。”
優化問題一般分為局部最優和全局最優。其中,
(1)局部最優,就是在函數值空間的一個有限區域內尋找最小值;而全局最優,是在函數值空間整個區域尋找最小值問題。
(2)函數局部最小點是它的函數值小於或等於附近點的點,但是有可能大於較遠距離的點。
(3)全局最小點是那種它的函數值小於或等於所有的可行點。
2.1.5 大數據與深度學習之間的關系
首先來看大數據、機器學習及數據挖掘三者簡單的定義:
大數據通常被定義為“超出常用軟件工具捕獲,管理和處理能力”的數據集。 機器學習關心的問題是如何構建計算機程序使用經驗自動改進。 數據挖掘是從數據中提取模式的特定算法的應用,在數據挖掘中,重點在於算法的應用,而不是算法本身。
機器學習和數據挖掘之間的關系如下: 數據挖掘是一個過程,在此過程中機器學習算法被用作提取數據集中的潛在有價值模式的工具。 大數據與深度學習關系總結如下:
(1)深度學習是一種模擬大腦的行為。可以從所學習對象的機制以及行為等等很多相關聯的方面進行學習,模仿類型行為以及思維。
(2)深度學習對於大數據的发展有幫助。深度學習對於大數據技術開发的每一個階段均有幫助,不管是數據的分析還是挖掘還是建模,只有深度學習,這些工作才會有可能一一得到實現。
(3)深度學習轉變了解決問題的思維。很多時候发現問題到解決問題,走一步看一步不是一個主要的解決問題的方式了,在深度學習的基礎上,要求我們從開始到最後都要基於一個目標,為了需要優化的那個最終目標去進行處理數據以及將數據放入到數據應用平台上去,這就是端到端(End to End)。
(4)大數據的深度學習需要一個框架。在大數據方面的深度學習都是從基礎的角度出发的,深度學習需要一個框架或者一個系統。總而言之,將你的大數據通過深度分析變為現實,這就是深度學習和大數據的最直接關系。
2.2 機器學習學習方式
根據數據類型的不同,對一個問題的建模有不同的方式。依據不同的學習方式和輸入數據,機器學習主要分為以下四種學習方式。
2.2.1 監督學習
特點:監督學習是使用已知正確答案的示例來訓練網絡。已知數據和其一一對應的標簽,訓練一個預測模型,將輸入數據映射到標簽的過程。
常見應用場景:監督式學習的常見應用場景如分類問題和回歸問題。
算法舉例:常見的有監督機器學習算法包括支持向量機(Support Vector Machine, SVM),樸素貝葉斯(Naive Bayes),邏輯回歸(Logistic Regression),K近鄰(K-Nearest Neighborhood, KNN),決策樹(Decision Tree),隨機森林(Random Forest),AdaBoost以及線性判別分析(Linear Discriminant Analysis, LDA)等。深度學習(Deep Learning)也是大多數以監督學習的方式呈現。
2.2.2 非監督式學習
定義:在非監督式學習中,數據並不被特別標識,適用於你具有數據集但無標簽的情況。學習模型是為了推斷出數據的一些內在結構。
常見應用場景:常見的應用場景包括關聯規則的學習以及聚類等。
算法舉例:常見算法包括Apriori算法以及k-Means算法。
2.2.3 半監督式學習
特點:在此學習方式下,輸入數據部分被標記,部分沒有被標記,這種學習模型可以用來進行預測。
常見應用場景:應用場景包括分類和回歸,算法包括一些對常用監督式學習算法的延伸,通過對已標記數據建模,在此基礎上,對未標記數據進行預測。
算法舉例:常見算法如圖論推理算法(Graph Inference)或者拉普拉斯支持向量機(Laplacian SVM)等。
2.2.4 弱監督學習
特點:弱監督學習可以看做是有多個標記的數據集合,次集合可以是空集,單個元素,或包含多種情況(沒有標記,有一個標記,和有多個標記)的多個元素。 數據集的標簽是不可靠的,這里的不可靠可以是標記不正確,多種標記,標記不充分,局部標記等。已知數據和其一一對應的弱標簽,訓練一個智能算法,將輸入數據映射到一組更強的標簽的過程。標簽的強弱指的是標簽蘊含的信息量的多少,比如相對於分割的標簽來說,分類的標簽就是弱標簽。
算法舉例:舉例,給出一張包含氣球的圖片,需要得出氣球在圖片中的位置及氣球和背景的分割線,這就是已知弱標簽學習強標簽的問題。
在企業數據應用的場景下, 人們最常用的可能就是監督式學習和非監督式學習的模型。 在圖像識別等領域,由於存在大量的非標識的數據和少量的可標識數據, 目前半監督式學習是一個很熱的話題。
2.2.5 監督學習有哪些步驟
監督學習是使用已知正確答案的示例來訓練網絡,每組訓練數據有一個明確的標識或結果。想象一下,我們可以訓練一個網絡,讓其從照片庫中(其中包含氣球的照片)識別出氣球的照片。以下就是我們在這個假設場景中所要采取的步驟。
步驟1:數據集的創建和分類 首先,瀏覽你的照片(數據集),確定所有包含氣球的照片,並對其進行標注。然後,將所有照片分為訓練集和驗證集。目標就是在深度網絡中找一函數,這個函數輸入是任意一張照片,當照片中包含氣球時,輸出1,否則輸出0。
步驟2:數據增強(Data Augmentation) 當原始數據搜集和標注完畢,一般搜集的數據並不一定包含目標在各種擾動下的信息。數據的好壞對於機器學習模型的預測能力至關重要,因此一般會進行數據增強。對於圖像數據來說,數據增強一般包括,圖像旋轉,平移,顏色變換,裁剪,仿射變換等。
步驟3:特征工程(Feature Engineering) 一般來講,特征工程包含特征提取和特征選擇。常見的手工特征(Hand-Crafted Feature)有尺度不變特征變換(Scale-Invariant Feature Transform, SIFT),方向梯度直方圖(Histogram of Oriented Gradient, HOG)等。由於手工特征是啟发式的,其算法設計背後的出发點不同,將這些特征組合在一起的時候有可能會產生沖突,如何將組合特征的效能发揮出來,使原始數據在特征空間中的判別性最大化,就需要用到特征選擇的方法。在深度學習方法大獲成功之後,人們很大一部分不再關注特征工程本身。因為,最常用到的卷積神經網絡(Convolutional Neural Networks, CNNs)本身就是一種特征提取和選擇的引擎。研究者提出的不同的網絡結構、正則化、歸一化方法實際上就是深度學習背景下的特征工程。
步驟4:構建預測模型和損失 將原始數據映射到特征空間之後,也就意味著我們得到了比較合理的輸入。下一步就是構建合適的預測模型得到對應輸入的輸出。而如何保證模型的輸出和輸入標簽的一致性,就需要構建模型預測和標簽之間的損失函數,常見的損失函數(Loss Function)有交叉熵、均方差等。通過優化方法不斷叠代,使模型從最初的初始化狀態一步步變化為有預測能力的模型的過程,實際上就是學習的過程。
步驟5:訓練 選擇合適的模型和超參數進行初始化,其中超參數比如支持向量機中核函數、誤差項懲罰權重等。當模型初始化參數設定好後,將制作好的特征數據輸入到模型,通過合適的優化方法不斷縮小輸出與標簽之間的差距,當叠代過程到了截止條件,就可以得到訓練好的模型。優化方法最常見的就是梯度下降法及其變種,使用梯度下降法的前提是優化目標函數對於模型是可導的。
步驟6:驗證和模型選擇 訓練完訓練集圖片後,需要進行模型測試。利用驗證集來驗證模型是否可以準確地挑選出含有氣球在內的照片。 在此過程中,通常會通過調整和模型相關的各種事物(超參數)來重覆步驟2和3,諸如里面有多少個節點,有多少層,使用怎樣的激活函數和損失函數,如何在反向傳播階段積極有效地訓練權值等等。
步驟7:測試及應用 當有了一個準確的模型,就可以將該模型部署到你的應用程序中。你可以將預測功能发布為API(Application Programming Interface, 應用程序編程接口)調用,並且你可以從軟件中調用該API,從而進行推理並給出相應的結果。
2.8 分類算法
分類算法和回歸算法是對真實世界不同建模的方法。分類模型是認為模型的輸出是離散的,例如大自然的生物被劃分為不同的種類,是離散的。回歸模型的輸出是連續的,例如人的身高變化過程是一個連續過程,而不是離散的。
因此,在實際建模過程時,采用分類模型還是回歸模型,取決於你對任務(真實世界)的分析和理解。
2.8.1 常用分類算法的優缺點?
接下來我們介紹常用分類算法的優缺點,如表2-1所示。
表2-1 常用分類算法的優缺點
| 算法 | 優點 | 缺點 |
|---|---|---|
| Bayes 貝葉斯分類法 | 1)所需估計的參數少,對於缺失數據不敏感。 2)有著堅實的數學基礎,以及穩定的分類效率。 |
1)需要假設屬性之間相互獨立,這往往並不成立。(喜歡吃番茄、雞蛋,卻不喜歡吃番茄炒蛋)。 2)需要知道先驗概率。 3)分類決策存在錯誤率。 |
| Decision Tree決策樹 | 1)不需要任何領域知識或參數假設。 2)適合高維數據。 3)簡單易於理解。 4)短時間內處理大量數據,得到可行且效果較好的結果。 5)能夠同時處理數據型和常規性屬性。 |
1)對於各類別樣本數量不一致數據,信息增益偏向於那些具有更多數值的特征。 2)易於過擬合。 3)忽略屬性之間的相關性。 4)不支持在線學習。 |
| SVM支持向量機 | 1)可以解決小樣本下機器學習的問題。 2)提高泛化性能。 3)可以解決高維、非線性問題。超高維文本分類仍受歡迎。 4)避免神經網絡結構選擇和局部極小的問題。 |
1)對缺失數據敏感。 2)內存消耗大,難以解釋。 3)運行和調參略煩人。 |
| KNN K近鄰 | 1)思想簡單,理論成熟,既可以用來做分類也可以用來做回歸; 2)可用於非線性分類; 3)訓練時間覆雜度為O(n); 4)準確度高,對數據沒有假設,對outlier不敏感; |
1)計算量太大。 2)對於樣本分類不均衡的問題,會產生誤判。 3)需要大量的內存。 4)輸出的可解釋性不強。 |
| Logistic Regression邏輯回歸 | 1)速度快。 2)簡單易於理解,直接看到各個特征的權重。 3)能容易地更新模型吸收新的數據。 4)如果想要一個概率框架,動態調整分類閥值。 |
特征處理覆雜。需要歸一化和較多的特征工程。 |
| Neural Network 神經網絡 | 1)分類準確率高。 2)並行處理能力強。 3)分布式存儲和學習能力強。 4)魯棒性較強,不易受噪聲影響。 |
1)需要大量參數(網絡拓撲、閥值、閾值)。 2)結果難以解釋。 3)訓練時間過長。 |
| Adaboosting | 1)adaboost是一種有很高精度的分類器。 2)可以使用各種方法構建子分類器,Adaboost算法提供的是框架。 3)當使用簡單分類器時,計算出的結果是可以理解的。而且弱分類器構造極其簡單。 4)簡單,不用做特征篩選。 5)不用擔心overfitting。 |
對outlier比較敏感 |
2.8.2 分類算法的評估方法
分類評估方法主要功能是用來評估分類算法的好壞,而評估一個分類器算法的好壞又包括許多項指標。了解各種評估方法,在實際應用中選擇正確的評估方法是十分重要的。
-
幾個常用術語 這里首先介紹幾個常見的模型評價術語,現在假設我們的分類目標只有兩類,計為正例(positive)和負例(negative)分別是: 1) True positives(TP): 被正確地劃分為正例的個數,即實際為正例且被分類器劃分為正例的實例數; 2) False positives(FP): 被錯誤地劃分為正例的個數,即實際為負例但被分類器劃分為正例的實例數; 3) False negatives(FN):被錯誤地劃分為負例的個數,即實際為正例但被分類器劃分為負例的實例數; 4) True negatives(TN): 被正確地劃分為負例的個數,即實際為負例且被分類器劃分為負例的實例數。
表2-2 四個術語的混淆矩陣
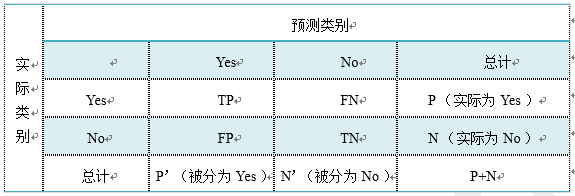
表2-2是這四個術語的混淆矩陣,做以下說明: 1)P=TP+FN表示實際為正例的樣本個數。 2)True、False描述的是分類器是否判斷正確。 3)Positive、Negative是分類器的分類結果,如果正例計為1、負例計為-1,即positive=1、negative=-1。用1表示True,-1表示False,那麽實際的類標=TF*PN,TF為true或false,PN為positive或negative。 4)例如True positives(TP)的實際類標=1*1=1為正例,False positives(FP)的實際類標=(-1)*1=-1為負例,False negatives(FN)的實際類標=(-1)*(-1)=1為正例,True negatives(TN)的實際類標=1*(-1)=-1為負例。
-
評價指標 1) 正確率(accuracy) 正確率是我們最常見的評價指標,accuracy = (TP+TN)/(P+N),正確率是被分對的樣本數在所有樣本數中的占比,通常來說,正確率越高,分類器越好。 2) 錯誤率(error rate) 錯誤率則與正確率相反,描述被分類器錯分的比例,error rate = (FP+FN)/(P+N),對某一個實例來說,分對與分錯是互斥事件,所以accuracy =1 - error rate。 3) 靈敏度(sensitivity) sensitivity = TP/P,表示的是所有正例中被分對的比例,衡量了分類器對正例的識別能力。 4) 特異性(specificity) specificity = TN/N,表示的是所有負例中被分對的比例,衡量了分類器對負例的識別能力。 5) 精度(precision) precision=TP/(TP+FP),精度是精確性的度量,表示被分為正例的示例中實際為正例的比例。 6) 召回率(recall) 召回率是覆蓋面的度量,度量有多個正例被分為正例,recall=TP/(TP+FN)=TP/P=sensitivity,可以看到召回率與靈敏度是一樣的。 7) 其他評價指標 計算速度:分類器訓練和預測需要的時間; 魯棒性:處理缺失值和異常值的能力; 可擴展性:處理大數據集的能力; 可解釋性:分類器的預測標準的可理解性,像決策樹產生的規則就是很容易理解的,而神經網絡的一堆參數就不好理解,我們只好把它看成一個黑盒子。 8) 精度和召回率反映了分類器分類性能的兩個方面。如果綜合考慮查準率與查全率,可以得到新的評價指標F1-score,也稱為綜合分類率:$F1=\frac{2 \times precision \times recall}{precision + recall}$。
為了綜合多個類別的分類情況,評測系統整體性能,經常采用的還有微平均F1(micro-averaging)和宏平均F1(macro-averaging )兩種指標。 (1)宏平均F1與微平均F1是以兩種不同的平均方式求的全局F1指標。 (2)宏平均F1的計算方法先對每個類別單獨計算F1值,再取這些F1值的算術平均值作為全局指標。 (3)微平均F1的計算方法是先累加計算各個類別的a、b、c、d的值,再由這些值求出F1值。 (4)由兩種平均F1的計算方式不難看出,宏平均F1平等對待每一個類別,所以它的值主要受到稀有類別的影響,而微平均F1平等考慮文檔集中的每一個文檔,所以它的值受到常見類別的影響比較大。 -
ROC曲線和PR曲線
如圖2-3,ROC曲線是(Receiver Operating Characteristic Curve,受試者工作特征曲線)的簡稱,是以靈敏度(真陽性率)為縱坐標,以1減去特異性(假陽性率)為橫坐標繪制的性能評價曲線。可以將不同模型對同一數據集的ROC曲線繪制在同一笛卡爾坐標系中,ROC曲線越靠近左上角,說明其對應模型越可靠。也可以通過ROC曲線下面的面積(Area Under Curve, AUC)來評價模型,AUC越大,模型越可靠。

圖2-3 ROC曲線
PR曲線是Precision Recall Curve的簡稱,描述的是precision和recall之間的關系,以recall為橫坐標,precision為縱坐標繪制的曲線。該曲線的所對應的面積AUC實際上是目標檢測中常用的評價指標平均精度(Average Precision, AP)。AP越高,說明模型性能越好。
2.8.3 正確率能很好的評估分類算法嗎
不同算法有不同特點,在不同數據集上有不同的表現效果,根據特定的任務選擇不同的算法。如何評價分類算法的好壞,要做具體任務具體分析。對於決策樹,主要用正確率去評估,但是其他算法,只用正確率能很好的評估嗎? 答案是否定的。 正確率確實是一個很直觀很好的評價指標,但是有時候正確率高並不能完全代表一個算法就好。比如對某個地區進行地震預測,地震分類屬性分為0:不发生地震、1发生地震。我們都知道,不发生的概率是極大的,對於分類器而言,如果分類器不加思考,對每一個測試樣例的類別都劃分為0,達到99%的正確率,但是,問題來了,如果真的发生地震時,這個分類器毫無察覺,那帶來的後果將是巨大的。很顯然,99%正確率的分類器並不是我們想要的。出現這種現象的原因主要是數據分布不均衡,類別為1的數據太少,錯分了類別1但達到了很高的正確率缺忽視了研究者本身最為關注的情況。
2.8.4 什麽樣的分類器是最好的
對某一個任務,某個具體的分類器不可能同時滿足或提高所有上面介紹的指標。 如果一個分類器能正確分對所有的實例,那麽各項指標都已經達到最優,但這樣的分類器往往不存在。比如之前說的地震預測,既然不能百分百預測地震的发生,但實際情況中能容忍一定程度的誤報。假設在1000次預測中,共有5次預測发生了地震,真實情況中有一次发生了地震,其他4次則為誤報。正確率由原來的999/1000=99.9下降為996/1000=99.6。召回率由0/1=0%上升為1/1=100%。對此解釋為,雖然預測失誤了4次,但真的地震发生前,分類器能預測對,沒有錯過,這樣的分類器實際意義更為重大,正是我們想要的。在這種情況下,在一定正確率前提下,要求分類器的召回率盡量高。
2.9 邏輯回歸
2.9.1 回歸劃分
廣義線性模型家族里,依據因變量不同,可以有如下劃分:
(1)如果是連續的,就是多重線性回歸。
(2)如果是二項分布,就是邏輯回歸。
(3)如果是泊松(Poisson)分布,就是泊松回歸。
(4)如果是負二項分布,就是負二項回歸。
(5)邏輯回歸的因變量可以是二分類的,也可以是多分類的,但是二分類的更為常用,也更加容易解釋。所以實際中最常用的就是二分類的邏輯回歸。
2.9.2 邏輯回歸適用性
邏輯回歸可用於以下幾個方面:
(1)用於概率預測。用於可能性預測時,得到的結果有可比性。比如根據模型進而預測在不同的自變量情況下,发生某病或某種情況的概率有多大。
(2)用於分類。實際上跟預測有些類似,也是根據模型,判斷某人屬於某病或屬於某種情況的概率有多大,也就是看一下這個人有多大的可能性是屬於某病。進行分類時,僅需要設定一個閾值即可,可能性高於閾值是一類,低於閾值是另一類。
(3)尋找危險因素。尋找某一疾病的危險因素等。
(4)僅能用於線性問題。只有當目標和特征是線性關系時,才能用邏輯回歸。在應用邏輯回歸時注意兩點:一是當知道模型是非線性時,不適用邏輯回歸;二是當使用邏輯回歸時,應注意選擇和目標為線性關系的特征。
(5)各特征之間不需要滿足條件獨立假設,但各個特征的貢獻獨立計算。
2.9.3 生成模型和判別模型的區別
生成模型:由數據學習聯合概率密度分布P(X,Y),然後求出條件概率分布P(Y|X)作為預測的模型,即生成模型:P(Y|X)= P(X,Y)/ P(X)(貝葉斯概率)。基本思想是首先建立樣本的聯合概率概率密度模型P(X,Y),然後再得到後驗概率P(Y|X),再利用它進行分類。典型的生成模型有樸素貝葉斯,隱馬爾科夫模型等
判別模型:由數據直接學習決策函數Y=f(X)或者條件概率分布P(Y|X)作為預測的模型,即判別模型。基本思想是有限樣本條件下建立判別函數,不考慮樣本的產生模型,直接研究預測模型。典型的判別模型包括k近鄰,感知級,決策樹,支持向量機等。這些模型的特點都是輸入屬性X可以直接得到後驗概率P(Y|X),輸出條件概率最大的作為最終的類別(對於二分類任務來說,實際得到一個score,當score大於threshold時則為正類,否則為負類)。
舉例:
判別式模型舉例:要確定一個羊是山羊還是綿羊,用判別模型的方法是從歷史數據中學習到模型,然後通過提取這只羊的特征來預測出這只羊是山羊的概率,是綿羊的概率。
生成式模型舉例:利用生成模型是根據山羊的特征首先學習出一個山羊的模型,然後根據綿羊的特征學習出一個綿羊的模型,然後從這只羊中提取特征,放到山羊模型中看概率是多少,在放到綿羊模型中看概率是多少,哪個大就是哪個。
聯系和區別:
生成方法的特點:上面說到,生成方法學習聯合概率密度分布P(X,Y),所以就可以從統計的角度表示數據的分布情況,能夠反映同類數據本身的相似度。但它不關心到底劃分各類的那個分類邊界在哪。生成方法可以還原出聯合概率分布P(Y,X),而判別方法不能。生成方法的學習收斂速度更快,即當樣本容量增加的時候,學到的模型可以更快的收斂於真實模型,當存在隱變量時,仍可以用生成方法學習。此時判別方法就不能用。 判別方法的特點:判別方法直接學習的是決策函數Y=f(X)或者條件概率分布P(Y|X)。不能反映訓練數據本身的特性。但它尋找不同類別之間的最優分類面,反映的是異類數據之間的差異。直接面對預測,往往學習的準確率更高。由於直接學習P(Y|X)或P(X),可以對數據進行各種程度上的抽象、定義特征並使用特征,因此可以簡化學習問題。 最後,由生成模型可以得到判別模型,但由判別模型得不到生成模型。
2.9.4 邏輯回歸與樸素貝葉斯有什麽區別
邏輯回歸與樸素貝葉斯區別有以下幾個方面:
(1)邏輯回歸是判別模型, 樸素貝葉斯是生成模型,所以生成和判別的所有區別它們都有。
(2)樸素貝葉斯屬於貝葉斯,邏輯回歸是最大似然,兩種概率哲學間的區別。
(3)樸素貝葉斯需要條件獨立假設。
(4)邏輯回歸需要求特征參數間是線性的。
2.9.5 線性回歸與邏輯回歸的區別
線性回歸與邏輯回歸的區別如下描述:
(1)線性回歸的樣本的輸出,都是連續值,$ y\in (-\infty ,+\infty )$,而邏輯回歸中$y\in (0,1)$,只能取0和1。
(2)對於擬合函數也有本質上的差別:
線性回歸:$f(x)=\theta ^{T}x=\theta _{1}x _{1}+\theta _{2}x _{2}+…+\theta _{n}x _{n}$
邏輯回歸:$f(x)=P(y=1|x;\theta )=g(\theta ^{T}x)$,其中,$g(z)=\frac{1}{1+e^{-z}}$
可以看出,線性回歸的擬合函數,是對f(x)的輸出變量y的擬合,而邏輯回歸的擬合函數是對為1類樣本的概率的擬合。
那麽,為什麽要以1類樣本的概率進行擬合呢,為什麽可以這樣擬合呢?
$\theta ^{T}x=0$就相當於是1類和0類的決策邊界:
當$\theta ^{T}x>0$,則y>0.5;若$\theta ^{T}x\rightarrow +\infty $,則$y \rightarrow 1 $,即y為1類;
當$\theta ^{T}x<0$,則y<0.5;若$\theta ^{T}x\rightarrow -\infty $,則$y \rightarrow 0 $,即y為0類;
這個時候就能看出區別,在線性回歸中$\theta ^{T}x$為預測值的擬合函數;而在邏輯回歸中$\theta ^{T}x$為決策邊界。下表2-3為線性回歸和邏輯回歸的區別。
表2-3 線性回歸和邏輯回歸的區別
| 線性回歸 | 邏輯回歸 | |
|---|---|---|
| 目的 | 預測 | 分類 |
| $y^{(i)}$ | 未知 | (0,1) |
| 函數 | 擬合函數 | 預測函數 |
| 參數計算方式 | 最小二乘法 | 極大似然估計 |
下面具體解釋一下:
- 擬合函數和預測函數什麽關系呢?簡單來說就是將擬合函數做了一個邏輯函數的轉換,轉換後使得$y^{(i)} \in (0,1)$;
- 最小二乘和最大似然估計可以相互替代嗎?回答當然是不行了。我們來看看兩者依仗的原理:最大似然估計是計算使得數據出現的可能性最大的參數,依仗的自然是Probability。而最小二乘是計算誤差損失。
2.10 代價函數
2.10.1 為什麽需要代價函數
- 為了得到訓練邏輯回歸模型的參數,需要一個代價函數,通過訓練代價函數來得到參數。
- 用於找到最優解的目的函數。
2.10.2 代價函數作用原理
在回歸問題中,通過代價函數來求解最優解,常用的是平方誤差代價函數。假設函數圖像如圖2-4所示,當參數发生變化時,假設函數狀態也會隨著變化。
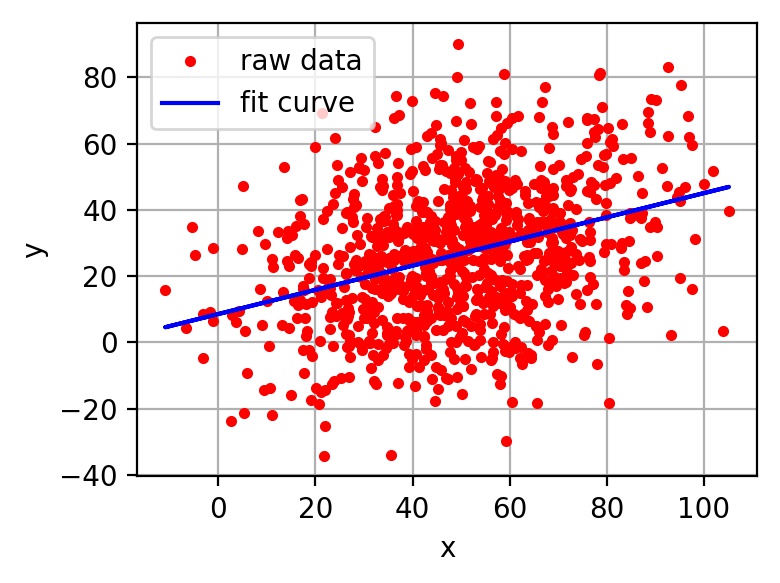
圖2-4 $h(x) = A + Bx$函數示意圖
想要擬合圖中的離散點,我們需要盡可能找到最優的$A$和$B$來使這條直線更能代表所有數據。如何找到最優解呢,這就需要使用代價函數來求解,以平方誤差代價函數為例,假設函數為$h(x)=\theta_0x$。 平方誤差代價函數的主要思想就是將實際數據給出的值與擬合出的線的對應值做差,求出擬合出的直線與實際的差距。在實際應用中,為了避免因個別極端數據產生的影響,采用類似方差再取二分之一的方式來減小個別數據的影響。因此,引出代價函數: \(J(\theta_0, \theta_1) = \frac{1}{m}\sum_{i=1}^m(h(x^{(i)})-y^{(i)})^2\)
最優解即為代價函數的最小值$\min J(\theta_0, \theta_1)$。如果是1個參數,代價函數一般通過二維曲線便可直觀看出。如果是2個參數,代價函數通過三維圖像可看出效果,參數越多,越覆雜。 當參數為2個時,代價函數是三維圖像,如下圖2-5所示。

圖2-5 代價函數三維圖像
2.10.3 為什麽代價函數要非負
目標函數存在一個下界,在優化過程當中,如果優化算法能夠使目標函數不斷減小,根據單調有界準則,這個優化算法就能證明是收斂有效的。 只要設計的目標函數有下界,基本上都可以,代價函數非負更為方便。
2.10.4 常見代價函數
(1)二次代價函數(quadratic cost): \(J = \frac{1}{2n}\sum_x\Vert y(x)-a^L(x)\Vert^2\)
其中,$J$表示代價函數,$x$表示樣本,$y$表示實際值,$a$表示輸出值,$n$表示樣本的總數。使用一個樣本為例簡單說明,此時二次代價函數為: \(J = \frac{(y-a)^2}{2}\) 假如使用梯度下降法(Gradient descent)來調整權值參數的大小,權值$w$和偏置$b$的梯度推導如下: \(\frac{\partial J}{\partial w}=(y-a)\sigma'(z)x\;, \frac{\partial J}{\partial b}=(y-a)\sigma'(z)\) 其中,$z$表示神經元的輸入,$\sigma$表示激活函數。權值$w$和偏置$b$的梯度跟激活函數的梯度成正比,激活函數的梯度越大,權值$w$和偏置$b$的大小調整得越快,訓練收斂得就越快。
注:神經網絡常用的激活函數為sigmoid函數,該函數的曲線如下圖2-6所示:
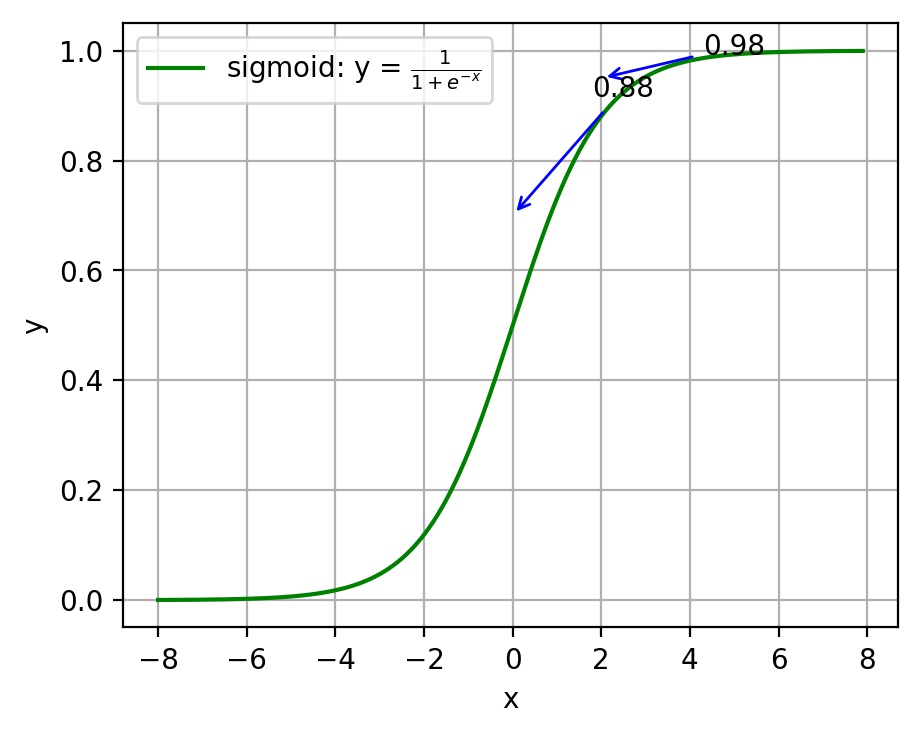
圖2-6 sigmoid函數曲線
如上圖所示,對0.88和0.98兩個點進行比較: 假設目標是收斂到1.0。0.88離目標1.0比較遠,梯度比較大,權值調整比較大。0.98離目標1.0比較近,梯度比較小,權值調整比較小。調整方案合理。 假如目標是收斂到0。0.88離目標0比較近,梯度比較大,權值調整比較大。0.98離目標0比較遠,梯度比較小,權值調整比較小。調整方案不合理。 原因:在使用sigmoid函數的情況下, 初始的代價(誤差)越大,導致訓練越慢。
(2)交叉熵代價函數(cross-entropy): \(J = -\frac{1}{n}\sum_x[y\ln a + (1-y)\ln{(1-a)}]\)
其中,$J$表示代價函數,$x$表示樣本,$y$表示實際值,$a$表示輸出值,$n$表示樣本的總數。 權值$w$和偏置$b$的梯度推導如下: \(\frac{\partial J}{\partial w_j}=\frac{1}{n}\sum_{x}x_j(\sigma{(z)}-y)\;, \frac{\partial J}{\partial b}=\frac{1}{n}\sum_{x}(\sigma{(z)}-y)\)
當誤差越大時,梯度就越大,權值$w$和偏置$b$調整就越快,訓練的速度也就越快。 二次代價函數適合輸出神經元是線性的情況,交叉熵代價函數適合輸出神經元是S型函數的情況。
(3)對數似然代價函數(log-likelihood cost):
對數似然函數常用來作為softmax回歸的代價函數。深度學習中普遍的做法是將softmax作為最後一層,此時常用的代價函數是對數似然代價函數。
對數似然代價函數與softmax的組合和交叉熵與sigmoid函數的組合非常相似。對數似然代價函數在二分類時可以化簡為交叉熵代價函數的形式。
在tensorflow中:
與sigmoid搭配使用的交叉熵函數:tf.nn.sigmoid_cross_entropy_with_logits()。
與softmax搭配使用的交叉熵函數:tf.nn.softmax_cross_entropy_with_logits()。
在pytorch中:
與sigmoid搭配使用的交叉熵函數:torch.nn.BCEWithLogitsLoss()。
與softmax搭配使用的交叉熵函數:torch.nn.CrossEntropyLoss()。
對數似然函數:
我們將似然函數作為機器學習模型的損失函數,並且用在分類問題中。這時似然函數是直接作用於模型的輸出的(損失函數就是為了衡量當前參數下model的預測值predict距離真實值label的大小,所以似然函數用作損失函數時當然也是為了完成該任務),所以對於似然函數來說,這里的樣本集就成了label集(而不是機器學習意義上的樣本集X了),這里的參數也不是機器學習model 的參數,而是predict值。
其實作為損失函數的似然函數並不關心你當前的機器學習model的參數是怎樣的,畢竟它此時所接收的輸入只有兩部分:1、predict。2、label 。3、分布模型(predict服從的分布)。
顯然這里的label就是似然函數的觀測值,即樣本集。而它眼里的模型,當然就是predict這個隨機變量所服從的概率分布模型。它的目的,就是衡量predict背後的模型對於當前觀測值的解釋程度。而每個樣本的predict值,恰恰就是它所服從的分布模型的參數。
比如此時我們的機器學習任務是一個4個類別的分類任務,機器學習model的輸出就是當前樣本X下的每個類別的概率,如predict=[0.1, 0.1, 0.7, 0.1],而該樣本的標簽是類別3,表示成向量就是label=[0, 0, 1, 0]。那麽label=[0, 0, 1, 0]就是似然函數眼里的樣本,然後我們可以假設predict這個隨機變量背後的模型是單次觀測下的多項式分布,(因為softmax本身是基於多項式分布的)。
回顧:
伯努利分布,也叫做(0,1)分布,貝努利分布可以看成是將一枚硬幣(只有正反兩個面,代表兩個類別)向上扔出,出現某個面(類別)的概率情況,因此其概率密度函數為:
\(f(x)=p^x(1-p)^{1-x}= \begin{cases} p,& x=1\\ q,& x=0 \end{cases}\) 這是理解似然函數做損失函數的關鍵!另外,貝努利分布的模型參數就是其中一個類別的发生概率。
而二項分布呢,就是將貝努利實驗重覆n次(各次實驗之間是相互獨立的)。
而多項式分布呢,就是將二項分布推廣到多個面(類別)。
所以,單次觀測下的多項式分布就是貝努利分布的多類推廣!即: \(f_{mulit}(x;p)=\prod_{i=1}^C p_{i}^{xi}\) 其中,C代表類別數。p代表向量形式的模型參數,即各個類別的发生概率,如p=[0.1, 0.1, 0.7, 0.1],則p1=0.1, p3=0.7等。即,多項式分布的模型參數就是各個類別的发生概率!x代表one-hot形式的觀測值,如x=類別3,則x=[0, 0, 1, 0]。xi代表x的第i個元素,比如x=類別3時,x1=0,x2=0,x3=1,x4=0。
想一下,機器學習model對某個樣本的輸出,就代表各個類別发生的概率。但是,對於當前這一個樣本而言,它肯定只能有一個類別,所以這一個樣本就可以看成是一次實驗(觀察),而這次實驗(觀察)的結果要服從上述各個類別发生的概率,那不就是服從多項式分布嘛!而且是單次觀察!各個類別发生的概率predict當然就是這個多項式分布的參數。
總結一下,對於多類分類問題,似然函數就是衡量當前這個以predict為參數的單次觀測下的多項式分布模型與樣本值label之間的似然度。
所以,根據似然函數的定義,單個樣本的似然函數即:
\(L = f_{mulit}(label;predict)\) 所以,整個樣本集(或者一個batch)的似然函數即: \(L=\prod_{X}f_{multi}(label;predict)= \prod_{X}\prod_{i=1}^{C}predict(i)^{label(i)}\) 所以在累乘號前面加上log函數後,就成了所謂的對數似然函數: \(L=\sum_{X}\sum_{i=1}^{C}label(i)log(predict(i))\) 而最大化對數似然函數就等效於最小化負對數似然函數,所以前面加個負號就和交叉熵的形式相同的了。
交叉熵定義:對於某種分布的隨機變量X~p(x), 有一個模型q(x)用於近似p(x)的概率分布,則分布X與模型q之間的交叉熵即:
\(H(X,q)=-\sum_{x}p(x)logq(x)\) 這里X的分布模型即樣本集label的真實分布模型,這里模型q(x)即想要模擬真實分布模型的機器學習模型。可以說交叉熵是直接衡量兩個分布,或者說兩個model之間的差異。而似然函數則是解釋以model的輸出為參數的某分布模型對樣本集的解釋程度。因此,可以說這兩者是“同貌不同源”,但是“殊途同歸”啦。
tips:
最大似然估計:
給定一堆數據,假如我們知道它是從某一種分布中隨機取出來的,可是我們並不知道這個分布具體的參,即“模型已定,參數未知”。例如,我們知道這個分布是正態分布,但是不知道均值和方差;或者是二項分布,但是不知道均值。最大似然估計(MLE,Maximum Likelihood Estimation)就可以用來估計模型的參數。MLE的目標是找出一組參數,使得模型產生出觀測數據的概率最大。
2.10.5 為什麽用交叉熵代替二次代價函數
(1)為什麽不用二次方代價函數 由上一節可知,權值$w$和偏置$b$的偏導數為$\frac{\partial J}{\partial w}=(a-y)\sigma’(z)x$,$\frac{\partial J}{\partial b}=(a-y)\sigma’(z)$, 偏導數受激活函數的導數影響,sigmoid函數導數在輸出接近0和1時非常小,會導致一些實例在剛開始訓練時學習得非常慢。
(2)為什麽要用交叉熵 交叉熵函數權值$w$和偏置$b$的梯度推導為: \(\frac{\partial J}{\partial w_j}=\frac{1}{n}\sum_{x}x_j(\sigma{(z)}-y)\;, \frac{\partial J}{\partial b}=\frac{1}{n}\sum_{x}(\sigma{(z)}-y)\)
由以上公式可知,權重學習的速度受到$\sigma{(z)}-y$影響,更大的誤差,就有更快的學習速度,避免了二次代價函數方程中因$\sigma’{(z)}$導致的學習緩慢的情況。
2.11 損失函數
2.11.1 什麽是損失函數
損失函數(Loss Function)又叫做誤差函數,用來衡量算法的運行情況,估量模型的預測值與真實值的不一致程度,是一個非負實值函數,通常使用$ L(Y, f(x))$來表示。損失函數越小,模型的魯棒性就越好。損失函數是經驗風險函數的核心部分,也是結構風險函數重要組成部分。
2.11.2 常見的損失函數
機器學習通過對算法中的目標函數進行不斷求解優化,得到最終想要的結果。分類和回歸問題中,通常使用損失函數或代價函數作為目標函數。 損失函數用來評價預測值和真實值不一樣的程度。通常損失函數越好,模型的性能也越好。 損失函數可分為經驗風險損失函數和結構風險損失函數。經驗風險損失函數指預測結果和實際結果的差別,結構風險損失函數是在經驗風險損失函數上加上正則項。 下面介紹常用的損失函數:
(1)0-1損失函數 如果預測值和目標值相等,值為0,如果不相等,值為1。 \(L(Y, f(x)) = \begin{cases} 1,& Y\ne f(x)\\ 0,& Y = f(x) \end{cases}\)
一般的在實際使用中,相等的條件過於嚴格,可適當放寬條件:
\[L(Y, f(x)) = \begin{cases} 1,& |Y-f(x)|\geqslant T\\ 0,& |Y-f(x)|< T \end{cases}\](2)絕對值損失函數 和0-1損失函數相似,絕對值損失函數表示為: \(L(Y, f(x)) = |Y-f(x)|\)
(3)平方損失函數 \(L(Y, f(x)) = \sum_N{(Y-f(x))}^2\)
這點可從最小二乘法和歐幾里得距離角度理解。最小二乘法的原理是,最優擬合曲線應該使所有點到回歸直線的距離和最小。
(4)對數損失函數 \(L(Y, P(Y|X)) = -\log{P(Y|X)}=-\frac{1}{N}\sum_{i=1}^N\sum_{j=1}^M y_{ij}log(p_{ij})\)
其中, Y 為輸出變量, X為輸入變量, L 為損失函數. N為輸入樣本量, M為可能的類別數, $y_{ij}$ 是一個二值指標, 表示類別 j 是否是輸入實例 xi 的真實類別. $p_{ij}$ 為模型或分類器預測輸入實例 xi 屬於類別 j 的概率.
常見的邏輯回歸使用的就是對數損失函數,有很多人認為邏輯回歸的損失函數是平方損失,其實不然。邏輯回歸它假設樣本服從伯努利分布(0-1分布),進而求得滿足該分布的似然函數,接著取對數求極值等。邏輯回歸推導出的經驗風險函數是最小化負的似然函數,從損失函數的角度看,就是對數損失函數。形式上等價於二分類的交叉熵損失函數。
(6)指數損失函數 指數損失函數的標準形式為: \(L(Y, f(x)) = \exp(-Yf(x))\)
例如AdaBoost就是以指數損失函數為損失函數。
(7)Hinge損失函數 Hinge損失函數的標準形式如下: \(L(y) = \max{(0, 1-ty)}\)
統一的形式: \(L(Y, f(x)) = \max{(0, Yf(x))}\)
其中y是預測值,範圍為(-1,1),t為目標值,其為-1或1。
在線性支持向量機中,最優化問題可等價於
\[\underset{\min}{w,b}\sum_{i=1}^N (1-y_i(wx_i+b))+\lambda\Vert w\Vert ^2\]上式相似於下式
\[\frac{1}{m}\sum_{i=1}^{N}l(wx_i+by_i) + \Vert w\Vert ^2\]其中$l(wx_i+by_i)$是Hinge損失函數,$\Vert w\Vert ^2$可看做為正則化項。
2.11.3 邏輯回歸為什麽使用對數損失函數
假設邏輯回歸模型 \(P(y=1|x;\theta)=\frac{1}{1+e^{-\theta^{T}x}}\) 假設邏輯回歸模型的概率分布是伯努利分布,其概率質量函數為: \(P(X=n)= \begin{cases} 1-p, n=0\\ p,n=1 \end{cases}\) 其似然函數為: \(L(\theta)=\prod_{i=1}^{m} P(y=1|x_i)^{y_i}P(y=0|x_i)^{1-y_i}\) 對數似然函數為: \(\ln L(\theta)=\sum_{i=1}^{m}[y_i\ln{P(y=1|x_i)}+(1-y_i)\ln{P(y=0|x_i)}]\\ =\sum_{i=1}^m[y_i\ln{P(y=1|x_i)}+(1-y_i)\ln(1-P(y=1|x_i))]\) 對數函數在單個數據點上的定義為: \(cost(y,p(y|x))=-y\ln{p(y|x)-(1-y)\ln(1-p(y|x))}\) 則全局樣本損失函數為: \(cost(y,p(y|x)) = -\sum_{i=1}^m[y_i\ln p(y_i|x_i)+(1-y_i)\ln(1-p(y_i|x_i))]\) 由此可看出,對數損失函數與極大似然估計的對數似然函數本質上是相同的。所以邏輯回歸直接采用對數損失函數。
2.11.4 對數損失函數是如何度量損失的
例如,在高斯分布中,我們需要確定均值和標準差。 如何確定這兩個參數?最大似然估計是比較常用的方法。最大似然的目標是找到一些參數值,這些參數值對應的分布可以最大化觀測到數據的概率。 因為需要計算觀測到所有數據的全概率,即所有觀測到的數據點的聯合概率。現考慮如下簡化情況:
(1)假設觀測到每個數據點的概率和其他數據點的概率是獨立的。
(2)取自然對數。 假設觀測到單個數據點$x_i(i=1,2,…n)$的概率為: \(P(x_i;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_i-\mu)^2}{2\sigma^2} \right)\)
(3)其聯合概率為: \(P(x_1,x_2,...,x_n;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_1-\mu)^2}{2\sigma^2} \right) \\ \times \frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_2-\mu)^2}{2\sigma^2} \right) \times ... \times \frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_n-\mu)^2}{2\sigma^2} \right)\) 對上式取自然對數,可得: \(\ln(P(x_1,x_2,...x_n;\mu,\sigma))= \ln \left(\frac{1}{\sigma \sqrt{2\pi}} \right) - \frac{(x_1-\mu)^2}{2\sigma^2} \\ + \ln \left( \frac{1}{\sigma \sqrt{2\pi}} \right) - \frac{(x_2-\mu)^2}{2\sigma^2} +...+ \ln \left( \frac{1}{\sigma \sqrt{2\pi}} \right) - \frac{(x_n-\mu)^2}{2\sigma^2}\) 根據對數定律,上式可以化簡為: \(\ln(P(x_1,x_2,...x_n;\mu,\sigma))=-n\ln(\sigma)-\frac{n}{2} \ln(2\pi)\\ -\frac{1}{2\sigma^2}[(x_1-\mu)^2+(x_2-\mu)^2+...+(x_n-\mu)^2]\) 然後求導為: \(\frac{\partial\ln(P(x_1,x_2,...,x_n;\mu,\sigma))}{\partial\mu}= \frac{n}{\sigma^2}[\mu - (x_1+x_2+...+x_n)]\) 上式左半部分為對數損失函數。損失函數越小越好,因此我們令等式左半的對數損失函數為0,可得: \(\mu=\frac{x_1+x_2+...+x_n}{n}\) 同理,可計算$\sigma $。
2.12 梯度下降
2.12.1 機器學習中為什麽需要梯度下降
梯度下降是機器學習中常見優化算法之一,梯度下降法有以下幾個作用:
(1)梯度下降是叠代法的一種,可以用於求解最小二乘問題。
(2)在求解機器學習算法的模型參數,即無約束優化問題時,主要有梯度下降法(Gradient Descent)和最小二乘法。
(3)在求解損失函數的最小值時,可以通過梯度下降法來一步步的叠代求解,得到最小化的損失函數和模型參數值。
(4)如果我們需要求解損失函數的最大值,可通過梯度上升法來叠代。梯度下降法和梯度上升法可相互轉換。
(5)在機器學習中,梯度下降法主要有隨機梯度下降法和批量梯度下降法。
2.12.2 梯度下降法缺點
梯度下降法缺點有以下幾點:
(1)靠近極小值時收斂速度減慢。
(2)直線搜索時可能會產生一些問題。
(3)可能會“之字形”地下降。
梯度概念也有需注意的地方:
(1)梯度是一個向量,即有方向有大小。
(2)梯度的方向是最大方向導數的方向。
(3)梯度的值是最大方向導數的值。
2.12.3 梯度下降法直觀理解
梯度下降法經典圖示如下圖2.7所示:
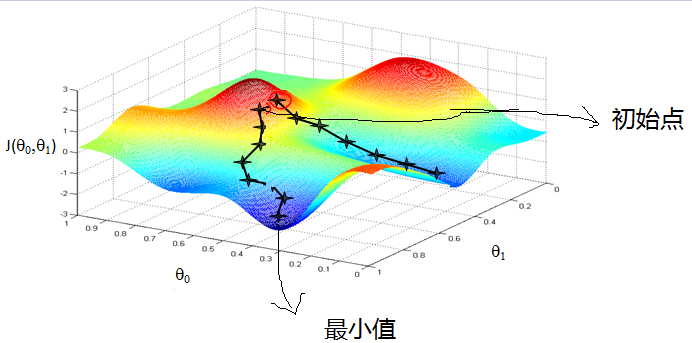
圖2.7 梯度下降法經典圖示
形象化舉例,由上圖2.7所示,假如最開始,我們在一座大山上的某處位置,因為到處都是陌生的,不知道下山的路,所以只能摸索著根據直覺,走一步算一步,在此過程中,每走到一個位置的時候,都會求解當前位置的梯度,沿著梯度的負方向,也就是當前最陡峭的位置向下走一步,然後繼續求解當前位置梯度,向這一步所在位置沿著最陡峭最易下山的位置走一步。不斷循環求梯度,就這樣一步步地走下去,一直走到我們覺得已經到了山腳。當然這樣走下去,有可能我們不能走到山腳,而是到了某一個局部的山勢低處。 由此,從上面的解釋可以看出,梯度下降不一定能夠找到全局的最優解,有可能是一個局部的最優解。當然,如果損失函數是凸函數,梯度下降法得到的解就一定是全局最優解。
核心思想歸納:
(1)初始化參數,隨機選取取值範圍內的任意數;
(2)叠代操作: a)計算當前梯度; b)修改新的變量; c)計算朝最陡的下坡方向走一步; d)判斷是否需要終止,如否,返回a);
(3)得到全局最優解或者接近全局最優解。
2.12.4 梯度下降法算法描述
梯度下降法算法步驟如下:
(1)確定優化模型的假設函數及損失函數。 舉例,對於線性回歸,假設函數為: \(h_\theta(x_1,x_2,...,x_n)=\theta_0+\theta_1x_1+...+\theta_nx_n\) 其中,$\theta_i,x_i(i=0,1,2,…,n)$分別為模型參數、每個樣本的特征值。 對於假設函數,損失函數為: \(J(\theta_0,\theta_1,...,\theta_n)=\frac{1}{2m}\sum^{m}_{j=0}(h_\theta (x^{(j)}_0 ,x^{(j)}_1,...,x^{(j)}_n)-y_j)^2\)
(2)相關參數初始化。 主要初始化${\theta}_i$、算法叠代步長${\alpha} $、終止距離${\zeta} $。初始化時可以根據經驗初始化,即${\theta} $初始化為0,步長${\alpha} $初始化為1。當前步長記為${\varphi}_i $。當然,也可隨機初始化。
(3)叠代計算。
1)計算當前位置時損失函數的梯度,對${\theta}_i $,其梯度表示為: \(\frac{\partial}{\partial \theta_i}J({\theta}_0,{\theta}_1,...,{\theta}_n)=\frac{1}{2m}\sum^{m}_{j=0}(h_\theta (x^{(j)}_0 ,x^{(j)}_1,...,x^{(j)}_n)-y_j)^2\) 2)計算當前位置下降的距離。 \({\varphi}_i={\alpha} \frac{\partial}{\partial \theta_i}J({\theta}_0,{\theta}_1,...,{\theta}_n)\) 3)判斷是否終止。 確定是否所有${\theta}_i$梯度下降的距離${\varphi}_i$都小於終止距離${\zeta}$,如果都小於${\zeta}$,則算法終止,當然的值即為最終結果,否則進入下一步。 4)更新所有的${\theta}_i$,更新後的表達式為: \({\theta}_i={\theta}_i-\alpha \frac{\partial}{\partial \theta_i}J({\theta}_0,{\theta}_1,...,{\theta}_n)\) \(\theta_i=\theta_i - \alpha \frac{1}{m} \sum^{m}_{j=0}(h_\theta (x^{(j)}_0 ,x^{(j)}_1,...,x^{(j)}_n)-y_j)x^{(j)}_i\) 5)令上式$x^{(j)}_0=1$,更新完畢後轉入1)。 由此,可看出,當前位置的梯度方向由所有樣本決定,上式中 $\frac{1}{m}$、$\alpha \frac{1}{m}$ 的目的是為了便於理解。
2.12.5 如何對梯度下降法進行調優
實際使用梯度下降法時,各項參數指標不能一步就達到理想狀態,對梯度下降法調優主要體現在以下幾個方面:
(1)算法叠代步長$\alpha$選擇。 在算法參數初始化時,有時根據經驗將步長初始化為1。實際取值取決於數據樣本。可以從大到小,多取一些值,分別運行算法看叠代效果,如果損失函數在變小,則取值有效。如果取值無效,說明要增大步長。但步長太大,有時會導致叠代速度過快,錯過最優解。步長太小,叠代速度慢,算法運行時間長。
(2)參數的初始值選擇。 初始值不同,獲得的最小值也有可能不同,梯度下降有可能得到的是局部最小值。如果損失函數是凸函數,則一定是最優解。由於有局部最優解的風險,需要多次用不同初始值運行算法,關鍵損失函數的最小值,選擇損失函數最小化的初值。
(3)標準化處理。 由於樣本不同,特征取值範圍也不同,導致叠代速度慢。為了減少特征取值的影響,可對特征數據標準化,使新期望為0,新方差為1,可節省算法運行時間。
2.12.6 隨機梯度和批量梯度區別
隨機梯度下降(SGD)和批量梯度下降(BGD)是兩種主要梯度下降法,其目的是增加某些限制來加速運算求解。 下面通過介紹兩種梯度下降法的求解思路,對其進行比較。 假設函數為: \(h_\theta (x_0,x_1,...,x_3) = \theta_0 x_0 + \theta_1 x_1 + ... + \theta_n x_n\) 損失函數為: \(J(\theta_0, \theta_1, ... , \theta_n) = \frac{1}{2m} \sum^{m}_{j=0}(h_\theta (x^{j}_0 ,x^{j}_1,...,x^{j}_n)-y^j)^2\) 其中,$m$為樣本個數,$j$為參數個數。
1、 批量梯度下降的求解思路如下: a) 得到每個$ \theta $對應的梯度: \(\frac{\partial}{\partial \theta_i}J({\theta}_0,{\theta}_1,...,{\theta}_n)=\frac{1}{m}\sum^{m}_{j=0}(h_\theta (x^{j}_0 ,x^{j}_1,...,x^{j}_n)-y^j)x^{j}_i\) b) 由於是求最小化風險函數,所以按每個參數 $ \theta $ 的梯度負方向更新 $ \theta_i $ : \(\theta_i=\theta_i - \frac{1}{m} \sum^{m}_{j=0}(h_\theta (x^{j}_0 ,x^{j}_1,...,x^{j}_n)-y^j)x^{j}_i\) c) 從上式可以注意到,它得到的雖然是一個全局最優解,但每叠代一步,都要用到訓練集所有的數據,如果樣本數據很大,這種方法叠代速度就很慢。 相比而言,隨機梯度下降可避免這種問題。
2、隨機梯度下降的求解思路如下: a) 相比批量梯度下降對應所有的訓練樣本,隨機梯度下降法中損失函數對應的是訓練集中每個樣本的粒度。 損失函數可以寫成如下這種形式, \(J(\theta_0, \theta_1, ... , \theta_n) = \frac{1}{m} \sum^{m}_{j=0}(y^j - h_\theta (x^{j}_0 ,x^{j}_1,...,x^{j}_n))^2 = \frac{1}{m} \sum^{m}_{j=0} cost(\theta,(x^j,y^j))\) b)對每個參數 $ \theta$ 按梯度方向更新 $ \theta$: \(\theta_i = \theta_i + (y^j - h_\theta (x^{j}_0, x^{j}_1, ... ,x^{j}_n))\) c) 隨機梯度下降是通過每個樣本來叠代更新一次。 隨機梯度下降伴隨的一個問題是噪音較批量梯度下降要多,使得隨機梯度下降並不是每次叠代都向著整體最優化方向。
小結: 隨機梯度下降法、批量梯度下降法相對來說都比較極端,簡單對比如下:
| 方法 | 特點 |
|---|---|
| 批量梯度下降 | a)采用所有數據來梯度下降。 b)批量梯度下降法在樣本量很大的時候,訓練速度慢。 |
| 隨機梯度下降 | a)隨機梯度下降用一個樣本來梯度下降。 b)訓練速度很快。 c)隨機梯度下降法僅僅用一個樣本決定梯度方向,導致解有可能不是全局最優。 d)收斂速度來說,隨機梯度下降法一次叠代一個樣本,導致叠代方向變化很大,不能很快的收斂到局部最優解。 |
下面介紹能結合兩種方法優點的小批量梯度下降法。
3、 小批量(Mini-Batch)梯度下降的求解思路如下 對於總數為$m$個樣本的數據,根據樣本的數據,選取其中的$n(1< n< m)$個子樣本來叠代。其參數$\theta$按梯度方向更新$\theta_i$公式如下: \(\theta_i = \theta_i - \alpha \sum^{t+n-1}_{j=t} ( h_\theta (x^{j}_{0}, x^{j}_{1}, ... , x^{j}_{n} ) - y^j ) x^{j}_{i}\)
2.12.7 各種梯度下降法性能比較
下表簡單對比隨機梯度下降(SGD)、批量梯度下降(BGD)、小批量梯度下降(Mini-batch GD)、和Online GD的區別:
| BGD | SGD | Mini-batch GD | Online GD | |
|---|---|---|---|---|
| 訓練集 | 固定 | 固定 | 固定 | 實時更新 |
| 單次叠代樣本數 | 整個訓練集 | 單個樣本 | 訓練集的子集 | 根據具體算法定 |
| 算法覆雜度 | 高 | 低 | 一般 | 低 |
| 時效性 | 低 | 一般 | 一般 | 高 |
| 收斂性 | 穩定 | 不穩定 | 較穩定 | 不穩定 |
BGD、SGD、Mini-batch GD,前面均已討論過,這里介紹一下Online GD。
Online GD於Mini-batch GD/SGD的區別在於,所有訓練數據只用一次,然後丟棄。這樣做的優點在於可預測最終模型的變化趨勢。
Online GD在互聯網領域用的較多,比如搜索廣告的點擊率(CTR)預估模型,網民的點擊行為會隨著時間改變。用普通的BGD算法(每天更新一次)一方面耗時較長(需要對所有歷史數據重新訓練);另一方面,無法及時反饋用戶的點擊行為遷移。而Online GD算法可以實時的依據網民的點擊行為進行遷移。
2.14 線性判別分析(LDA)
2.14.1 LDA思想總結
線性判別分析(Linear Discriminant Analysis,LDA)是一種經典的降維方法。和主成分分析PCA不考慮樣本類別輸出的無監督降維技術不同,LDA是一種監督學習的降維技術,數據集的每個樣本有類別輸出。
LDA分類思想簡單總結如下:
- 多維空間中,數據處理分類問題較為覆雜,LDA算法將多維空間中的數據投影到一條直線上,將d維數據轉化成1維數據進行處理。
- 對於訓練數據,設法將多維數據投影到一條直線上,同類數據的投影點盡可能接近,異類數據點盡可能遠離。
- 對數據進行分類時,將其投影到同樣的這條直線上,再根據投影點的位置來確定樣本的類別。
如果用一句話概括LDA思想,即“投影後類內方差最小,類間方差最大”。
2.14.2 圖解LDA核心思想
假設有紅、藍兩類數據,這些數據特征均為二維,如下圖所示。我們的目標是將這些數據投影到一維,讓每一類相近的數據的投影點盡可能接近,不同類別數據盡可能遠,即圖中紅色和藍色數據中心之間的距離盡可能大。
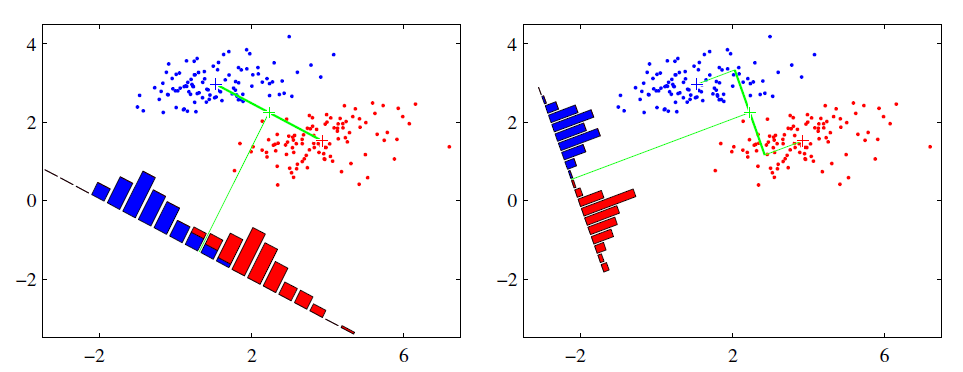
左圖和右圖是兩種不同的投影方式。
左圖思路:讓不同類別的平均點距離最遠的投影方式。
右圖思路:讓同類別的數據挨得最近的投影方式。
從上圖直觀看出,右圖紅色數據和藍色數據在各自的區域來說相對集中,根據數據分布直方圖也可看出,所以右圖的投影效果好於左圖,左圖中間直方圖部分有明顯交集。
以上例子是基於數據是二維的,分類後的投影是一條直線。如果原始數據是多維的,則投影後的分類面是一低維的超平面。
2.14.3 二類LDA算法原理
輸入:數據集 $D={(\boldsymbol x_1,\boldsymbol y_1),(\boldsymbol x_2,\boldsymbol y_2),…,(\boldsymbol x_m,\boldsymbol y_m)}$,其中樣本 $\boldsymbol x_i $ 是n維向量,$\boldsymbol y_i \epsilon {0, 1}$,降維後的目標維度 $d$。定義
$N_j(j=0,1)$ 為第 $j$ 類樣本個數;
$X_j(j=0,1)$ 為第 $j$ 類樣本的集合;
$u_j(j=0,1)$ 為第 $j$ 類樣本的均值向量;
$\sum_j(j=0,1)$ 為第 $j$ 類樣本的協方差矩陣。
其中 \(u_j = \frac{1}{N_j} \sum_{\boldsymbol x\epsilon X_j}\boldsymbol x(j=0,1), \sum_j = \sum_{\boldsymbol x\epsilon X_j}(\boldsymbol x-u_j)(\boldsymbol x-u_j)^T(j=0,1)\) 假設投影直線是向量 $\boldsymbol w$,對任意樣本 $\boldsymbol x_i$,它在直線 $w$上的投影為 $\boldsymbol w^Tx_i$,兩個類別的中心點 $u_0$, $u_1 $在直線 $w$ 的投影分別為 $\boldsymbol w^Tu_0$ 、$\boldsymbol w^Tu_1$。
LDA的目標是讓兩類別的數據中心間的距離 $| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 |^2_2$ 盡量大,與此同時,希望同類樣本投影點的協方差$\boldsymbol w^T \sum_0 \boldsymbol w$、$\boldsymbol w^T \sum_1 \boldsymbol w$ 盡量小,最小化 $\boldsymbol w^T \sum_0 \boldsymbol w + \boldsymbol w^T \sum_1 \boldsymbol w$ 。 定義 類內散度矩陣 \(S_w = \sum_0 + \sum_1 = \sum_{\boldsymbol x\epsilon X_0}(\boldsymbol x-u_0)(\boldsymbol x-u_0)^T + \sum_{\boldsymbol x\epsilon X_1}(\boldsymbol x-u_1)(\boldsymbol x-u_1)^T\) 類間散度矩陣 $S_b = (u_0 - u_1)(u_0 - u_1)^T$
據上分析,優化目標為 \(\mathop{\arg\max}_\boldsymbol w J(\boldsymbol w) = \frac{\| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|^2_2}{\boldsymbol w^T \sum_0\boldsymbol w + \boldsymbol w^T \sum_1\boldsymbol w} = \frac{\boldsymbol w^T(u_0-u_1)(u_0-u_1)^T\boldsymbol w}{\boldsymbol w^T(\sum_0 + \sum_1)\boldsymbol w} = \frac{\boldsymbol w^TS_b\boldsymbol w}{\boldsymbol w^TS_w\boldsymbol w}\) 根據廣義瑞利商的性質,矩陣 \(S^{-1}_{w}S_b\) 的最大特征值為 $J(\boldsymbol w)$ 的最大值,矩陣 $S^{-1}_{w}S_b$ 的最大特征值對應的特征向量即為 $(\boldsymbol w)$。
2.14.4 LDA算法流程總結
LDA算法降維流程如下:
輸入:數據集 $D = { (x_1,y_1),(x_2,y_2), … ,(x_m,y_m) }$,其中樣本 $x_i $ 是n維向量,$y_i \epsilon {C_1, C_2, …, C_k}$,降維後的目標維度 $d$ 。
輸出:降維後的數據集 $\overline{D} $ 。
步驟:
- 計算類內散度矩陣 $S_w$。
- 計算類間散度矩陣 $S_b$ 。
- 計算矩陣 $S^{-1}_wS_b$ 。
- 計算矩陣 $S^{-1}_wS_b$ 的最大的 d 個特征值。
- 計算 d 個特征值對應的 d 個特征向量,記投影矩陣為 W 。
- 轉化樣本集的每個樣本,得到新樣本 $P_i = W^Tx_i$ 。
- 輸出新樣本集 $\overline{D} = { (p_1,y_1),(p_2,y_2),…,(p_m,y_m) }$
2.14.5 LDA和PCA區別
| 異同點 | LDA | PCA |
|---|---|---|
| 相同點 | 1. 兩者均可以對數據進行降維; 2. 兩者在降維時均使用了矩陣特征分解的思想; 3. 兩者都假設數據符合高斯分布; |
|
| 不同點 | 有監督的降維方法; | 無監督的降維方法; |
| 降維最多降到k-1維; | 降維多少沒有限制; | |
| 可以用於降維,還可以用於分類; | 只用於降維; | |
| 選擇分類性能最好的投影方向; | 選擇樣本點投影具有最大方差的方向; | |
| 更明確,更能反映樣本間差異; | 目的較為模糊; |
2.14.6 LDA優缺點
| 優缺點 | 簡要說明 |
|---|---|
| 優點 | 1. 可以使用類別的先驗知識; 2. 以標簽、類別衡量差異性的有監督降維方式,相對於PCA的模糊性,其目的更明確,更能反映樣本間的差異; |
| 缺點 | 1. LDA不適合對非高斯分布樣本進行降維; 2. LDA降維最多降到分類數k-1維; 3. LDA在樣本分類信息依賴方差而不是均值時,降維效果不好; 4. LDA可能過度擬合數據。 |
2.15 主成分分析(PCA)
2.15.1 主成分分析(PCA)思想總結
- PCA就是將高維的數據通過線性變換投影到低維空間上去。
- 投影思想:找出最能夠代表原始數據的投影方法。被PCA降掉的那些維度只能是那些噪聲或是冗余的數據。
- 去冗余:去除可以被其他向量代表的線性相關向量,這部分信息量是多余的。
- 去噪聲,去除較小特征值對應的特征向量,特征值的大小反映了變換後在特征向量方向上變換的幅度,幅度越大,說明這個方向上的元素差異也越大,要保留。
- 對角化矩陣,尋找極大線性無關組,保留較大的特征值,去除較小特征值,組成一個投影矩陣,對原始樣本矩陣進行投影,得到降維後的新樣本矩陣。
- 完成PCA的關鍵是——協方差矩陣。協方差矩陣,能同時表現不同維度間的相關性以及各個維度上的方差。協方差矩陣度量的是維度與維度之間的關系,而非樣本與樣本之間。
- 之所以對角化,因為對角化之後非對角上的元素都是0,達到去噪聲的目的。對角化後的協方差矩陣,對角線上較小的新方差對應的就是那些該去掉的維度。所以我們只取那些含有較大能量(特征值)的維度,其余的就舍掉,即去冗余。
2.15.2 圖解PCA核心思想
PCA可解決訓練數據中存在數據特征過多或特征累贅的問題。核心思想是將m維特征映射到n維(n < m),這n維形成主元,是重構出來最能代表原始數據的正交特征。
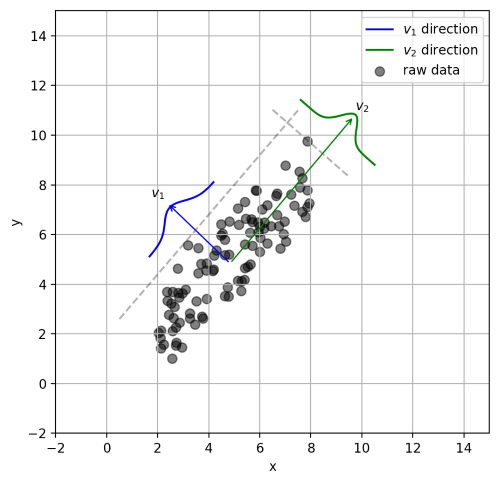
假設數據集是m個n維,$(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \cdots, \boldsymbol x^{(m)})$。如果$n=2$,需要降維到$n’=1$,現在想找到某一維度方向代表這兩個維度的數據。下圖有$u_1, u_2$兩個向量方向,但是哪個向量才是我們所想要的,可以更好代表原始數據集的呢?
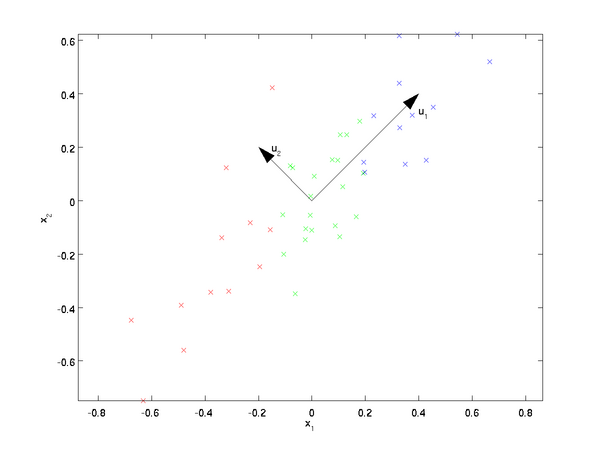
從圖可看出,$u_1$比$u_2$好,為什麽呢?有以下兩個主要評價指標:
- 樣本點到這個直線的距離足夠近。
- 樣本點在這個直線上的投影能盡可能的分開。
如果我們需要降維的目標維數是其他任意維,則:
- 樣本點到這個超平面的距離足夠近。
- 樣本點在這個超平面上的投影能盡可能的分開。
2.15.3 PCA算法推理
下面以基於最小投影距離為評價指標推理:
假設數據集是m個n維,$(x^{(1)}, x^{(2)},…,x^{(m)})$,且數據進行了中心化。經過投影變換得到新坐標為 ${w_1,w_2,…,w_n}$,其中 $w$ 是標準正交基,即 $| w |_2 = 1$,$w^T_iw_j = 0$。
經過降維後,新坐標為 ${ w_1,w_2,…,w_n }$,其中 $n’$ 是降維後的目標維數。樣本點 $x^{(i)}$ 在新坐標系下的投影為 \(z^{(i)} = \left(z^{(i)}_1, z^{(i)}_2, ..., z^{(i)}_{n'} \right)\),其中 $z^{(i)}_j = w^T_j x^{(i)}$ 是 $x^{(i)} $ 在低維坐標系里第 j 維的坐標。
如果用 $z^{(i)} $ 去恢覆 $x^{(i)} $ ,則得到的恢覆數據為 $\widehat{x}^{(i)} = \sum^{n’}_{j=1} x^{(i)}_j w_j = Wz^{(i)}$,其中 $W$為標準正交基組成的矩陣。
考慮到整個樣本集,樣本點到這個超平面的距離足夠近,目標變為最小化 $\sum^m_{i=1} | \hat{x}^{(i)} - x^{(i)} |^2_2$ 。對此式進行推理,可得: \(\sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2 = \sum^m_{i=1} \| Wz^{(i)} - x^{(i)} \|^2_2 \\ = \sum^m_{i=1} \left( Wz^{(i)} \right)^T \left( Wz^{(i)} \right) - 2\sum^m_{i=1} \left( Wz^{(i)} \right)^T x^{(i)} + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = \sum^m_{i=1} \left( z^{(i)} \right)^T \left( z^{(i)} \right) - 2\sum^m_{i=1} \left( z^{(i)} \right)^T x^{(i)} + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = - \sum^m_{i=1} \left( z^{(i)} \right)^T \left( z^{(i)} \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = -tr \left( W^T \left( \sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T \right)W \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = -tr \left( W^TXX^TW \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)}\)
在推導過程中,分別用到了 $\overline{x}^{(i)} = Wz^{(i)}$ ,矩陣轉置公式 $(AB)^T = B^TA^T$,$W^TW = I$,$z^{(i)} = W^Tx^{(i)}$ 以及矩陣的跡,最後兩步是將代數和轉為矩陣形式。 由於 $W$ 的每一個向量 $w_j$ 是標準正交基,$\sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T$ 是數據集的協方差矩陣,$\sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} $ 是一個常量。最小化 $\sum^m_{i=1} | \hat{x}^{(i)} - x^{(i)} |^2_2$ 又可等價於 \(\underbrace{\arg \min}_W - tr \left( W^TXX^TW \right) s.t.W^TW = I\) 利用拉格朗日函數可得到 \(J(W) = -tr(W^TXX^TW) + \lambda(W^TW - I)\) 對 $W$ 求導,可得 $-XX^TW + \lambda W = 0 $ ,也即 $ XX^TW = \lambda W $ 。 $ XX^T $ 是 $ n’ $ 個特征向量組成的矩陣,$\lambda$ 為$ XX^T $ 的特征值。$W$ 即為我們想要的矩陣。 對於原始數據,只需要 $z^{(i)} = W^TX^{(i)}$ ,就可把原始數據集降維到最小投影距離的 $n’$ 維數據集。
基於最大投影方差的推導,這里就不再贅述,有興趣的同仁可自行查閱資料。
2.15.4 PCA算法流程總結
輸入:$n$ 維樣本集 $D = \left( x^{(1)},x^{(2)},…,x^{(m)} \right)$ ,目標降維的維數 $n’$ 。
輸出:降維後的新樣本集 $D’ = \left( z^{(1)},z^{(2)},…,z^{(m)} \right)$ 。
主要步驟如下:
- 對所有的樣本進行中心化,$ x^{(i)} = x^{(i)} - \frac{1}{m} \sum^m_{j=1} x^{(j)} $ 。
- 計算樣本的協方差矩陣 $XX^T$ 。
- 對協方差矩陣 $XX^T$ 進行特征值分解。
- 取出最大的 $n’ $ 個特征值對應的特征向量 ${ w_1,w_2,…,w_{n’} }$ 。
- 標準化特征向量,得到特征向量矩陣 $W$ 。
- 轉化樣本集中的每個樣本 $z^{(i)} = W^T x^{(i)}$ 。
- 得到輸出矩陣 $D’ = \left( z^{(1)},z^{(2)},…,z^{(n)} \right)$ 。 注:在降維時,有時不明確目標維數,而是指定降維到的主成分比重閾值 $k(k \epsilon(0,1])$ 。假設 $n$ 個特征值為 $\lambda_1 \geqslant \lambda_2 \geqslant … \geqslant \lambda_n$ ,則 $n’$ 可從 \(\sum^{n'}_{i=1} \lambda_i \geqslant k \times \sum^n_{i=1} \lambda_i\) 得到。
2.15.5 PCA算法主要優缺點
| 優缺點 | 簡要說明 |
|---|---|
| 優點 | 1.僅僅需要以方差衡量信息量,不受數據集以外的因素影響。 2.各主成分之間正交,可消除原始數據成分間的相互影響的因素。 3.計算方法簡單,主要運算是特征值分解,易於實現。 |
| 缺點 | 1.主成分各個特征維度的含義具有一定的模糊性,不如原始樣本特征的解釋性強。 2.方差小的非主成分也可能含有對樣本差異的重要信息,因降維丟棄可能對後續數據處理有影響。 |
2.15.6 降維的必要性及目的
降維的必要性:
- 多重共線性和預測變量之間相互關聯。多重共線性會導致解空間的不穩定,從而可能導致結果的不連貫。
- 高維空間本身具有稀疏性。一維正態分布有68%的值落於正負標準差之間,而在十維空間上只有2%。
- 過多的變量,對查找規律造成冗余麻煩。
- 僅在變量層面上分析可能會忽略變量之間的潛在聯系。例如幾個預測變量可能落入僅反映數據某一方面特征的一個組內。
降維的目的:
- 減少預測變量的個數。
- 確保這些變量是相互獨立的。
- 提供一個框架來解釋結果。相關特征,特別是重要特征更能在數據中明確的顯示出來;如果只有兩維或者三維的話,更便於可視化展示。
- 數據在低維下更容易處理、更容易使用。
- 去除數據噪聲。
- 降低算法運算開銷。
2.15.7 KPCA與PCA的區別
應用PCA算法前提是假設存在一個線性超平面,進而投影。那如果數據不是線性的呢?該怎麽辦?這時候就需要KPCA,數據集從 $n$ 維映射到線性可分的高維 $N >n$,然後再從 $N$ 維降維到一個低維度 $n’(n’<n<N)$ 。
KPCA用到了核函數思想,使用了核函數的主成分分析一般稱為核主成分分析(Kernelized PCA, 簡稱KPCA)。
假設高維空間數據由 $n$ 維空間的數據通過映射 $\phi$ 產生。
$n$ 維空間的特征分解為: \(\sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T W = \lambda W\)
其映射為 \(\sum^m_{i=1} \phi \left( x^{(i)} \right) \phi \left( x^{(i)} \right)^T W = \lambda W\)
通過在高維空間進行協方差矩陣的特征值分解,然後用和PCA一樣的方法進行降維。由於KPCA需要核函數的運算,因此它的計算量要比PCA大很多。
2.16 模型評估
2.16.1 模型評估常用方法?
一般情況來說,單一評分標準無法完全評估一個機器學習模型。只用good和bad偏離真實場景去評估某個模型,都是一種欠妥的評估方式。下面介紹常用的分類模型和回歸模型評估方法。
分類模型常用評估方法:
| 指標 | 描述 |
|---|---|
| Accuracy | 準確率 |
| Precision | 精準度/查準率 |
| Recall | 召回率/查全率 |
| P-R曲線 | 查準率為縱軸,查全率為橫軸,作圖 |
| F1 | F1值 |
| Confusion Matrix | 混淆矩陣 |
| ROC | ROC曲線 |
| AUC | ROC曲線下的面積 |
回歸模型常用評估方法:
| 指標 | 描述 |
|---|---|
| Mean Square Error (MSE, RMSE) | 平均方差 |
| Absolute Error (MAE, RAE) | 絕對誤差 |
| R-Squared | R平方值 |
2.16.2 誤差、偏差和方差有什麽區別和聯系
在機器學習中,Bias(偏差),Error(誤差),和Variance(方差)存在以下區別和聯系:
對於Error::
-
誤差(error):一般地,我們把學習器的實際預測輸出與樣本的真是輸出之間的差異稱為“誤差”。
-
Error = Bias + Variance + Noise,Error反映的是整個模型的準確度。
對於Noise:
噪聲:描述了在當前任務上任何學習算法所能達到的期望泛化誤差的下界,即刻畫了學習問題本身的難度。
對於Bias:
- Bias衡量模型擬合訓練數據的能力(訓練數據不一定是整個 training dataset,而是只用於訓練它的那一部分數據,例如:mini-batch),Bias反映的是模型在樣本上的輸出與真實值之間的誤差,即模型本身的精準度。
- Bias 越小,擬合能力越高(可能產生overfitting);反之,擬合能力越低(可能產生underfitting)。
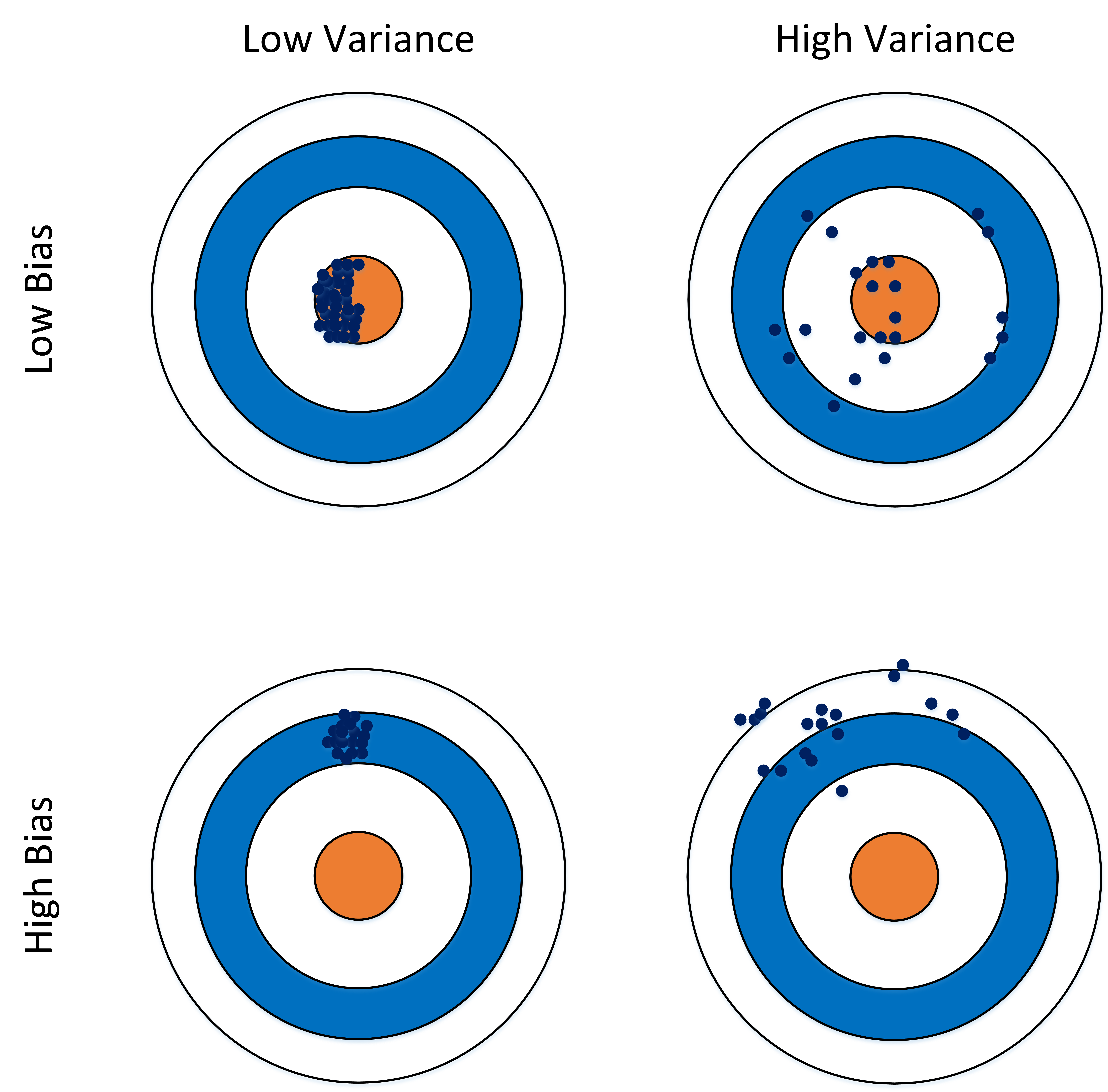
- 偏差越大,越偏離真實數據,如下圖第二行所示。
對於Variance:
-
方差公式:$S_{N}^{2}=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}$
- Variance描述的是預測值的變化範圍,離散程度,也就是離其期望值的距離。方差越大,數據的分布越分散,模型的穩定程度越差。
- Variance反映的是模型每一次輸出結果與模型輸出期望之間的誤差,即模型的穩定性。
- Variance越小,模型的泛化的能力越高;反之,模型的泛化的能力越低。
- 如果模型在訓練集上擬合效果比較優秀,但是在測試集上擬合效果比較差劣,則方差較大,說明模型的穩定程度較差,出現這種現象可能是由於模型對訓練集過擬合造成的。 如下圖右列所示。
2.16.3 經驗誤差與泛化誤差
經驗誤差(empirical error):也叫訓練誤差(training error),模型在訓練集上的誤差。
泛化誤差(generalization error):模型在新樣本集(測試集)上的誤差稱為“泛化誤差”。
2.16.4 圖解欠擬合、過擬合
根據不同的坐標方式,欠擬合與過擬合圖解不同。
- 橫軸為訓練樣本數量,縱軸為誤差
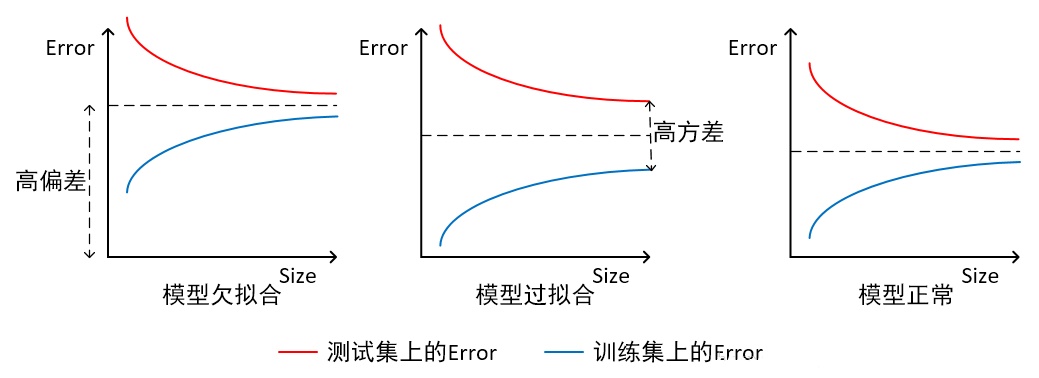
如上圖所示,我們可以直觀看出欠擬合和過擬合的區別:
模型欠擬合:在訓練集以及測試集上同時具有較高的誤差,此時模型的偏差較大;
模型過擬合:在訓練集上具有較低的誤差,在測試集上具有較高的誤差,此時模型的方差較大。
模型正常:在訓練集以及測試集上,同時具有相對較低的偏差以及方差。
- 橫軸為模型覆雜程度,縱軸為誤差
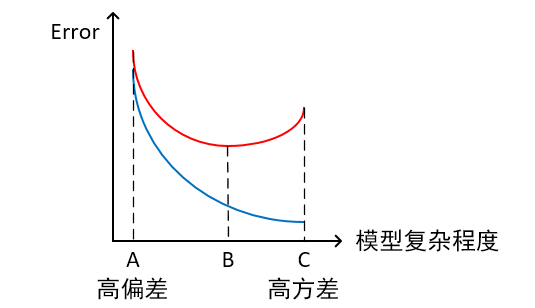
紅線為測試集上的Error,藍線為訓練集上的Error
模型欠擬合:模型在點A處,在訓練集以及測試集上同時具有較高的誤差,此時模型的偏差較大。
模型過擬合:模型在點C處,在訓練集上具有較低的誤差,在測試集上具有較高的誤差,此時模型的方差較大。
模型正常:模型覆雜程度控制在點B處為最優。
- 橫軸為正則項系數,縱軸為誤差
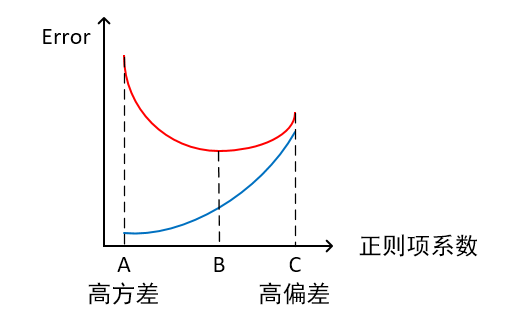
紅線為測試集上的Error,藍線為訓練集上的Error
模型欠擬合:模型在點C處,在訓練集以及測試集上同時具有較高的誤差,此時模型的偏差較大。
模型過擬合:模型在點A處,在訓練集上具有較低的誤差,在測試集上具有較高的誤差,此時模型的方差較大。 它通常发生在模型過於覆雜的情況下,如參數過多等,會使得模型的預測性能變弱,並且增加數據的波動性。雖然模型在訓練時的效果可以表現的很完美,基本上記住了數據的全部特點,但這種模型在未知數據的表現能力會大減折扣,因為簡單的模型泛化能力通常都是很弱的。
模型正常:模型覆雜程度控制在點B處為最優。
2.16.5 如何解決過擬合與欠擬合
如何解決欠擬合:
- 添加其他特征項。組合、泛化、相關性、上下文特征、平台特征等特征是特征添加的重要手段,有時候特征項不夠會導致模型欠擬合。
- 添加多項式特征。例如將線性模型添加二次項或三次項使模型泛化能力更強。例如,FM(Factorization Machine)模型、FFM(Field-aware Factorization Machine)模型,其實就是線性模型,增加了二階多項式,保證了模型一定的擬合程度。
- 可以增加模型的覆雜程度。
- 減小正則化系數。正則化的目的是用來防止過擬合的,但是現在模型出現了欠擬合,則需要減少正則化參數。
如何解決過擬合:
- 重新清洗數據,數據不純會導致過擬合,此類情況需要重新清洗數據。
- 增加訓練樣本數量。
- 降低模型覆雜程度。
- 增大正則項系數。
- 采用dropout方法,dropout方法,通俗的講就是在訓練的時候讓神經元以一定的概率不工作。
- early stopping。
- 減少叠代次數。
- 增大學習率。
- 添加噪聲數據。
- 樹結構中,可以對樹進行剪枝。
- 減少特征項。
欠擬合和過擬合這些方法,需要根據實際問題,實際模型,進行選擇。
2.16.6 交叉驗證的主要作用
為了得到更為穩健可靠的模型,對模型的泛化誤差進行評估,得到模型泛化誤差的近似值。當有多個模型可以選擇時,我們通常選擇“泛化誤差”最小的模型。
交叉驗證的方法有許多種,但是最常用的是:留一交叉驗證、k折交叉驗證。
2.16.7 理解k折交叉驗證
- 將含有N個樣本的數據集,分成K份,每份含有N/K個樣本。選擇其中1份作為測試集,另外K-1份作為訓練集,測試集就有K種情況。
- 在每種情況中,用訓練集訓練模型,用測試集測試模型,計算模型的泛化誤差。
- 交叉驗證重覆K次,每份驗證一次,平均K次的結果或者使用其它結合方式,最終得到一個單一估測,得到模型最終的泛化誤差。
- 將K種情況下,模型的泛化誤差取均值,得到模型最終的泛化誤差。
- 一般$2\leqslant K \leqslant10$。 k折交叉驗證的優勢在於,同時重覆運用隨機產生的子樣本進行訓練和驗證,每次的結果驗證一次,10折交叉驗證是最常用的。
- 訓練集中樣本數量要足夠多,一般至少大於總樣本數的50%。
- 訓練集和測試集必須從完整的數據集中均勻取樣。均勻取樣的目的是希望減少訓練集、測試集與原數據集之間的偏差。當樣本數量足夠多時,通過隨機取樣,便可以實現均勻取樣的效果。
2.16.8 混淆矩陣
第一種混淆矩陣:
| 真實情況T or F | 預測為正例1,P | 預測為負例0,N |
|---|---|---|
| 本來label標記為1,預測結果真為T、假為F | TP(預測為1,實際為1) | FN(預測為0,實際為1) |
| 本來label標記為0,預測結果真為T、假為F | FP(預測為1,實際為0) | TN(預測為0,實際也為0) |
第二種混淆矩陣:
| 預測情況P or N | 實際label為1,預測對了為T | 實際label為0,預測對了為T |
|---|---|---|
| 預測為正例1,P | TP(預測為1,實際為1) | FP(預測為1,實際為0) |
| 預測為負例0,N | FN(預測為0,實際為1) | TN(預測為0,實際也為0) |
2.16.9 錯誤率及精度
- 錯誤率(Error Rate):分類錯誤的樣本數占樣本總數的比例。
- 精度(accuracy):分類正確的樣本數占樣本總數的比例。
2.16.10 查準率與查全率
將算法預測的結果分成四種情況:
- 正確肯定(True Positive,TP):預測為真,實際為真
- 正確否定(True Negative,TN):預測為假,實際為假
- 錯誤肯定(False Positive,FP):預測為真,實際為假
- 錯誤否定(False Negative,FN):預測為假,實際為真
則:
查準率(Precision)=TP/(TP+FP)
理解:預測出為陽性的樣本中,正確的有多少。區別準確率(正確預測出的樣本,包括正確預測為陽性、陰性,占總樣本比例)。 例,在所有我們預測有惡性腫瘤的病人中,實際上有惡性腫瘤的病人的百分比,越高越好。
查全率(Recall)=TP/(TP+FN)
理解:正確預測為陽性的數量占總樣本中陽性數量的比例。 例,在所有實際上有惡性腫瘤的病人中,成功預測有惡性腫瘤的病人的百分比,越高越好。
2.16.11 ROC與AUC
ROC全稱是“受試者工作特征”(Receiver Operating Characteristic)。
ROC曲線的面積就是AUC(Area Under Curve)。
AUC用於衡量“二分類問題”機器學習算法性能(泛化能力)。
ROC曲線,通過將連續變量設定出多個不同的臨界值,從而計算出一系列真正率和假正率,再以假正率為橫坐標、真正率為縱坐標繪制成曲線,曲線下面積越大,推斷準確性越高。在ROC曲線上,最靠近坐標圖左上方的點為假正率和真正率均較高的臨界值。
對於分類器,或者說分類算法,評價指標主要有Precision,Recall,F-score。下圖是一個ROC曲線的示例。
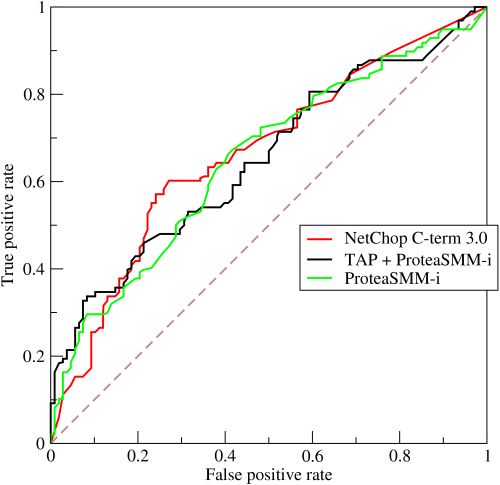
ROC曲線的橫坐標為False Positive Rate(FPR),縱坐標為True Positive Rate(TPR)。其中 \(TPR = \frac{TP}{TP+FN} ,FPR = \frac{FP}{FP+TN}\)
下面著重介紹ROC曲線圖中的四個點和一條線。 第一個點(0,1),即FPR=0, TPR=1,這意味著FN(False Negative)=0,並且FP(False Positive)=0。意味著這是一個完美的分類器,它將所有的樣本都正確分類。 第二個點(1,0),即FPR=1,TPR=0,意味著這是一個最糟糕的分類器,因為它成功避開了所有的正確答案。 第三個點(0,0),即FPR=TPR=0,即FP(False Positive)=TP(True Positive)=0,可以发現該分類器預測所有的樣本都為負樣本(Negative)。 第四個點(1,1),即FPR=TPR=1,分類器實際上預測所有的樣本都為正樣本。 經過以上分析,ROC曲線越接近左上角,該分類器的性能越好。
ROC曲線所覆蓋的面積稱為AUC(Area Under Curve),可以更直觀的判斷學習器的性能,AUC越大則性能越好。
2.16.12 如何畫ROC曲線
下圖是一個示例,圖中共有20個測試樣本,“Class”一欄表示每個測試樣本真正的標簽(p表示正樣本,n表示負樣本),“Score”表示每個測試樣本屬於正樣本的概率。
步驟: 1、假設已經得出一系列樣本被劃分為正類的概率,按照大小排序。 2、從高到低,依次將“Score”值作為閾值threshold,當測試樣本屬於正樣本的概率大於或等於這個threshold時,我們認為它為正樣本,否則為負樣本。舉例來說,對於圖中的第4個樣本,其“Score”值為0.6,那麽樣本1,2,3,4都被認為是正樣本,因為它們的“Score”值都大於等於0.6,而其他樣本則都認為是負樣本。 3、每次選取一個不同的threshold,得到一組FPR和TPR,即ROC曲線上的一點。以此共得到20組FPR和TPR的值。 4、根據3、中的每個坐標點,畫圖。
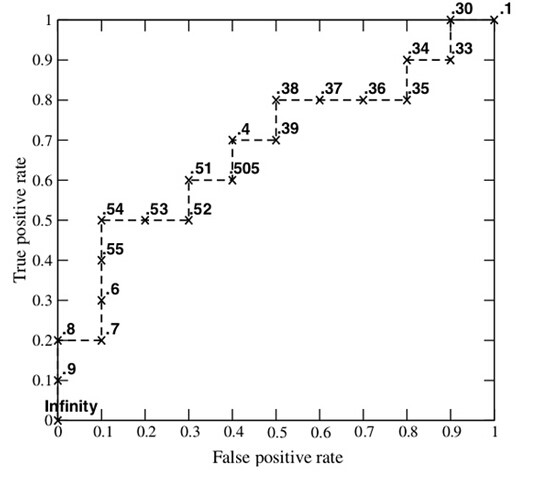
2.16.13 如何計算TPR,FPR
1、分析數據 y_true = [0, 0, 1, 1];scores = [0.1, 0.4, 0.35, 0.8]; 2、列表
| 樣本 | 預測屬於P的概率(score) | 真實類別 |
|---|---|---|
| y[0] | 0.1 | N |
| y[1] | 0.4 | N |
| y[2] | 0.35 | P |
| y[3] | 0.8 | P |
3、將截斷點依次取為score值,計算TPR和FPR。 當截斷點為0.1時: 說明只要score>=0.1,它的預測類別就是正例。 因為4個樣本的score都大於等於0.1,所以,所有樣本的預測類別都為P。 scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [1, 1, 1, 1]; 正例與反例信息如下:
| 正例 | 反例 | |
|---|---|---|
| 正例 | TP=2 | FN=0 |
| 反例 | FP=2 | TN=0 |
由此可得: TPR = TP/(TP+FN) = 1; FPR = FP/(TN+FP) = 1;
當截斷點為0.35時: scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [0, 1, 1, 1]; 正例與反例信息如下:
| 正例 | 反例 | |
|---|---|---|
| 正例 | TP=2 | FN=0 |
| 反例 | FP=1 | TN=1 |
由此可得: TPR = TP/(TP+FN) = 1; FPR = FP/(TN+FP) = 0.5;
當截斷點為0.4時: scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [0, 1, 0, 1]; 正例與反例信息如下:
| 正例 | 反例 | |
|---|---|---|
| 正例 | TP=1 | FN=1 |
| 反例 | FP=1 | TN=1 |
由此可得: TPR = TP/(TP+FN) = 0.5; FPR = FP/(TN+FP) = 0.5;
當截斷點為0.8時: scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [0, 0, 0, 1];
正例與反例信息如下:
| 正例 | 反例 | |
|---|---|---|
| 正例 | TP=1 | FN=1 |
| 反例 | FP=0 | TN=2 |
由此可得: TPR = TP/(TP+FN) = 0.5; FPR = FP/(TN+FP) = 0;
4、根據TPR、FPR值,以FPR為橫軸,TPR為縱軸畫圖。
2.16.14 如何計算AUC
- 將坐標點按照橫坐標FPR排序 。
- 計算第$i$個坐標點和第$i+1$個坐標點的間距$dx$ 。
- 獲取第$i$或者$i+1$個坐標點的縱坐標y。
- 計算面積微元$ds=ydx$。
- 對面積微元進行累加,得到AUC。
2.16.15 為什麽使用Roc和Auc評價分類器
模型有很多評估方法,為什麽還要使用ROC和AUC呢? 因為ROC曲線有個很好的特性:當測試集中的正負樣本的分布變換的時候,ROC曲線能夠保持不變。在實際的數據集中經常會出現樣本類不平衡,即正負樣本比例差距較大,而且測試數據中的正負樣本也可能隨著時間變化。
2.16.16 直觀理解AUC
下圖展現了三種AUC的值:
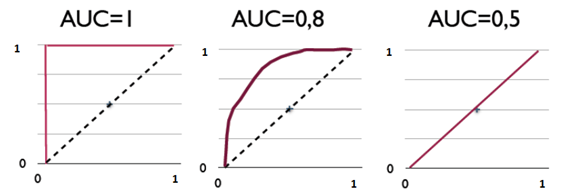
AUC是衡量二分類模型優劣的一種評價指標,表示正例排在負例前面的概率。其他評價指標有精確度、準確率、召回率,而AUC比這三者更為常用。 一般在分類模型中,預測結果都是以概率的形式表現,如果要計算準確率,通常都會手動設置一個閾值來將對應的概率轉化成類別,這個閾值也就很大程度上影響了模型準確率的計算。 舉例: 現在假設有一個訓練好的二分類器對10個正負樣本(正例5個,負例5個)預測,得分按高到低排序得到的最好預測結果為[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],即5個正例均排在5個負例前面,正例排在負例前面的概率為100%。然後繪制其ROC曲線,由於是10個樣本,除去原點我們需要描10個點,如下:
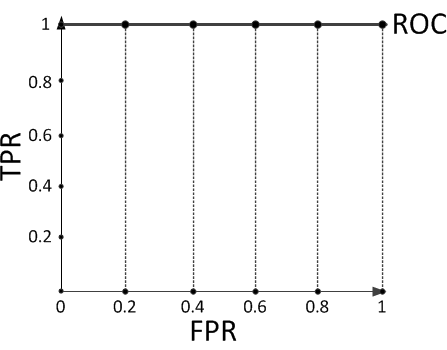
描點方式按照樣本預測結果的得分高低從左至右開始遍歷。從原點開始,每遇到1便向y軸正方向移動y軸最小步長1個單位,這里是1/5=0.2;每遇到0則向x軸正方向移動x軸最小步長1個單位,這里也是0.2。不難看出,上圖的AUC等於1,印證了正例排在負例前面的概率的確為100%。
假設預測結果序列為[1, 1, 1, 1, 0, 1, 0, 0, 0, 0]。
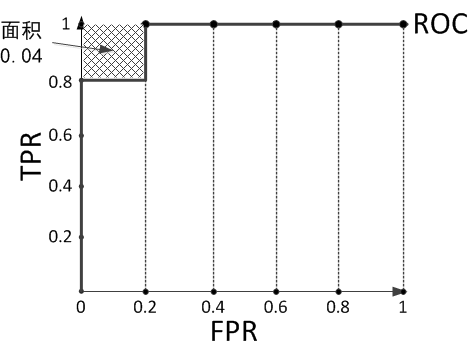
計算上圖的AUC為0.96與計算正例與排在負例前面的概率0.8 × 1 + 0.2 × 0.8 = 0.96相等,而左上角陰影部分的面積則是負例排在正例前面的概率0.2 × 0.2 = 0.04。
假設預測結果序列為[1, 1, 1, 0, 1, 0, 1, 0, 0, 0]。
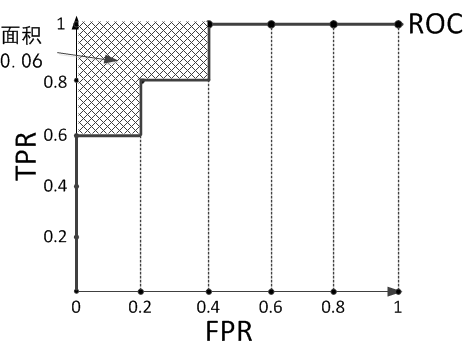
計算上圖的AUC為0.88與計算正例與排在負例前面的概率0.6 × 1 + 0.2 × 0.8 + 0.2 × 0.6 = 0.88相等,左上角陰影部分的面積是負例排在正例前面的概率0.2 × 0.2 × 3 = 0.12。
2.16.17 代價敏感錯誤率與代價曲線
不同的錯誤會產生不同代價。以二分法為例,設置代價矩陣如下:

當判斷正確的時候,值為0,不正確的時候,分別為$Cost_{01}$和$Cost_{10}$ 。
$Cost_{10}$:表示實際為反例但預測成正例的代價。
$Cost_{01}$:表示實際為正例但是預測為反例的代價。
代價敏感錯誤率=樣本中由模型得到的錯誤值與代價乘積之和 / 總樣本。 其數學表達式為: \(E(f;D;cost)=\frac{1}{m}\left( \sum_{x_{i} \in D^{+}}({f(x_i)\neq y_i})\times Cost_{01}+ \sum_{x_{i} \in D^{-}}({f(x_i)\neq y_i})\times Cost_{10}\right)\) $D^{+}、D^{-}$分別代表樣例集的正例子集和反例子集,x是預測值,y是真實值。
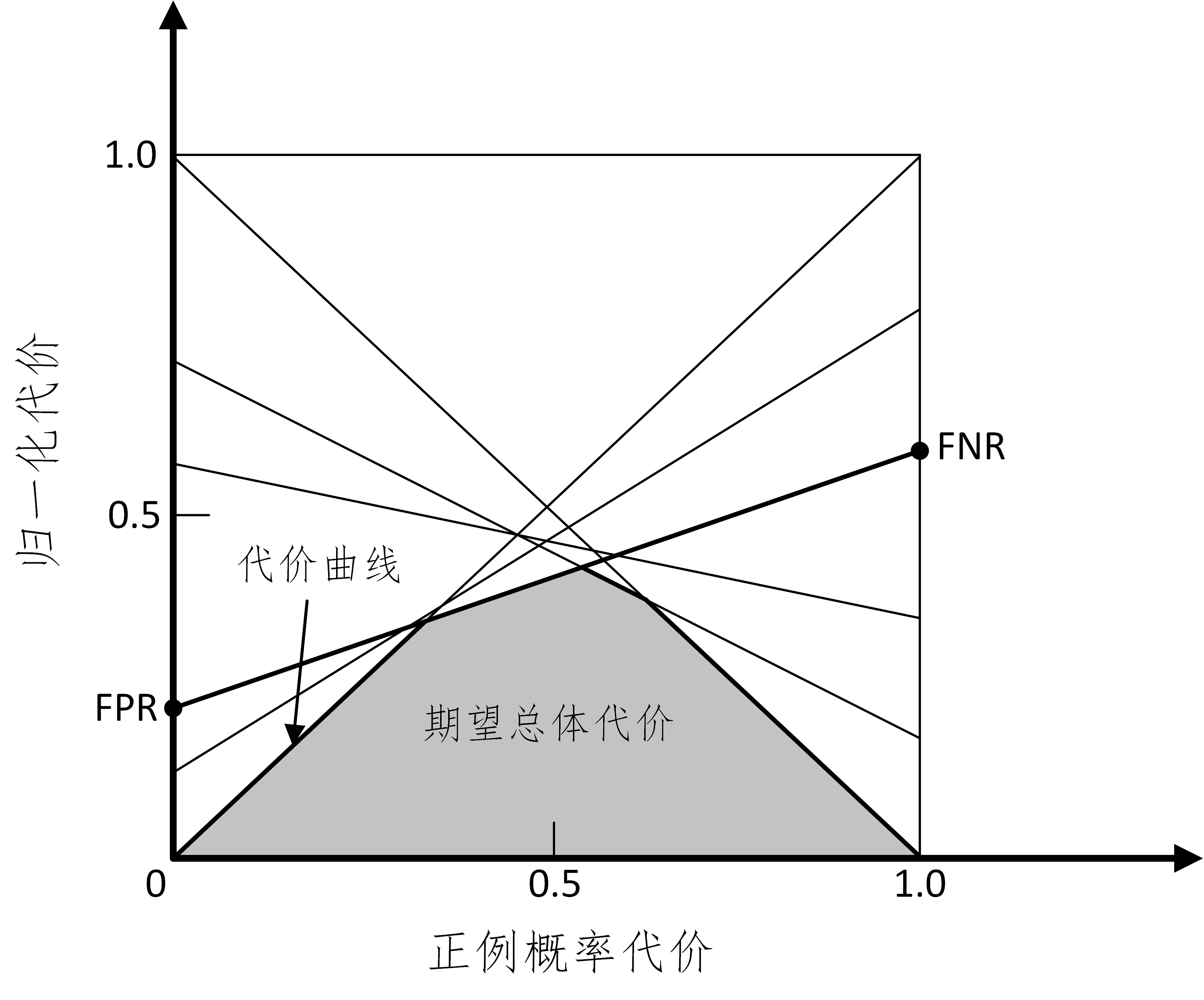
代價曲線: 在均等代價時,ROC曲線不能直接反應出模型的期望總體代價,而代價曲線可以。 代價曲線橫軸為[0,1]的正例函數代價: \(P(+)Cost=\frac{p*Cost_{01}}{p*Cost_{01}+(1-p)*Cost_{10}}\) 其中p是樣本為正例的概率。
代價曲線縱軸維[0,1]的歸一化代價: \(Cost_{norm}=\frac{FNR*p*Cost_{01}+FNR*(1-p)*Cost_{10}}{p*Cost_{01}+(1-p)*Cost_{10}}\)
其中FPR為假陽率,FNR=1-TPR為假陰率。
注:ROC每個點,對應代價平面上一條線。
例如,ROC上(TPR,FPR),計算出FNR=1-TPR,在代價平面上繪制一條從(0,FPR)到(1,FNR)的線段,面積則為該條件下期望的總體代價。所有線段下界面積,所有條件下學習器的期望總體代價。
2.16.18 模型有哪些比較檢驗方法
正確性分析:模型穩定性分析,穩健性分析,收斂性分析,變化趨勢分析,極值分析等。 有效性分析:誤差分析,參數敏感性分析,模型對比檢驗等。 有用性分析:關鍵數據求解,極值點,拐點,變化趨勢分析,用數據驗證動態模擬等。 高效性分析:時空覆雜度分析與現有進行比較等。
2.16.19 為什麽使用標準差
方差公式為:$S_{N}^{2}=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}$
標準差公式為:$S_{N}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}}$
樣本標準差公式為:$S_{N}=\sqrt{\frac{1}{N-1}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}}$
與方差相比,使用標準差來表示數據點的離散程度有3個好處: 1、表示離散程度的數字與樣本數據點的數量級一致,更適合對數據樣本形成感性認知。
2、表示離散程度的數字單位與樣本數據的單位一致,更方便做後續的分析運算。
3、在樣本數據大致符合正態分布的情況下,標準差具有方便估算的特性:68%的數據點落在平均值前後1個標準差的範圍內、95%的數據點落在平均值前後2個標準差的範圍內,而99%的數據點將會落在平均值前後3個標準差的範圍內。
2.16.20 類別不平衡產生原因
類別不平衡(class-imbalance)是指分類任務中不同類別的訓練樣例數目差別很大的情況。
產生原因:
分類學習算法通常都會假設不同類別的訓練樣例數目基本相同。如果不同類別的訓練樣例數目差別很大,則會影響學習結果,測試結果變差。例如二分類問題中有998個反例,正例有2個,那學習方法只需返回一個永遠將新樣本預測為反例的分類器,就能達到99.8%的精度;然而這樣的分類器沒有價值。
2.16.21 常見的類別不平衡問題解決方法
防止類別不平衡對學習造成的影響,在構建分類模型之前,需要對分類不平衡性問題進行處理。主要解決方法有:
1、擴大數據集
增加包含小類樣本數據的數據,更多的數據能得到更多的分布信息。
2、對大類數據欠采樣
減少大類數據樣本個數,使與小樣本個數接近。 缺點:欠采樣操作時若隨機丟棄大類樣本,可能會丟失重要信息。 代表算法:EasyEnsemble。其思想是利用集成學習機制,將大類劃分為若幹個集合供不同的學習器使用。相當於對每個學習器都進行欠采樣,但對於全局則不會丟失重要信息。
3、對小類數據過采樣
過采樣:對小類的數據樣本進行采樣來增加小類的數據樣本個數。
代表算法:SMOTE和ADASYN。
SMOTE:通過對訓練集中的小類數據進行插值來產生額外的小類樣本數據。
新的少數類樣本產生的策略:對每個少數類樣本a,在a的最近鄰中隨機選一個樣本b,然後在a、b之間的連線上隨機選一點作為新合成的少數類樣本。 ADASYN:根據學習難度的不同,對不同的少數類別的樣本使用加權分布,對於難以學習的少數類的樣本,產生更多的綜合數據。 通過減少類不平衡引入的偏差和將分類決策邊界自適應地轉移到困難的樣本兩種手段,改善了數據分布。
4、使用新評價指標
如果當前評價指標不適用,則應尋找其他具有說服力的評價指標。比如準確度這個評價指標在類別不均衡的分類任務中並不適用,甚至進行誤導。因此在類別不均衡分類任務中,需要使用更有說服力的評價指標來對分類器進行評價。
5、選擇新算法
不同的算法適用於不同的任務與數據,應該使用不同的算法進行比較。
6、數據代價加權
例如當分類任務是識別小類,那麽可以對分類器的小類樣本數據增加權值,降低大類樣本的權值,從而使得分類器將重點集中在小類樣本身上。
7、轉化問題思考角度
例如在分類問題時,把小類的樣本作為異常點,將問題轉化為異常點檢測或變化趨勢檢測問題。 異常點檢測即是對那些罕見事件進行識別。變化趨勢檢測區別於異常點檢測在於其通過檢測不尋常的變化趨勢來識別。
8、將問題細化分析
對問題進行分析與挖掘,將問題劃分成多個更小的問題,看這些小問題是否更容易解決。
2.17 決策樹
2.17.1 決策樹的基本原理
決策樹(Decision Tree)是一種分而治之的決策過程。一個困難的預測問題,通過樹的分支節點,被劃分成兩個或多個較為簡單的子集,從結構上劃分為不同的子問題。將依規則分割數據集的過程不斷遞歸下去(Recursive Partitioning)。隨著樹的深度不斷增加,分支節點的子集越來越小,所需要提的問題數也逐漸簡化。當分支節點的深度或者問題的簡單程度滿足一定的停止規則(Stopping Rule)時, 該分支節點會停止分裂,此為自上而下的停止閾值(Cutoff Threshold)法;有些決策樹也使用自下而上的剪枝(Pruning)法。
2.17.2 決策樹的三要素?
一棵決策樹的生成過程主要分為下3個部分:
1、特征選擇:從訓練數據中眾多的特征中選擇一個特征作為當前節點的分裂標準,如何選擇特征有著很多不同量化評估標準,從而衍生出不同的決策樹算法。
2、決策樹生成:根據選擇的特征評估標準,從上至下遞歸地生成子節點,直到數據集不可分則決策樹停止生長。樹結構來說,遞歸結構是最容易理解的方式。
3、剪枝:決策樹容易過擬合,一般來需要剪枝,縮小樹結構規模、緩解過擬合。剪枝技術有預剪枝和後剪枝兩種。
2.17.3 決策樹學習基本算法

2.17.4 決策樹算法優缺點
決策樹算法的優點:
1、決策樹算法易理解,機理解釋起來簡單。
2、決策樹算法可以用於小數據集。
3、決策樹算法的時間覆雜度較小,為用於訓練決策樹的數據點的對數。
4、相比於其他算法智能分析一種類型變量,決策樹算法可處理數字和數據的類別。
5、能夠處理多輸出的問題。
6、對缺失值不敏感。
7、可以處理不相關特征數據。
8、效率高,決策樹只需要一次構建,反覆使用,每一次預測的最大計算次數不超過決策樹的深度。
決策樹算法的缺點:
1、對連續性的字段比較難預測。
2、容易出現過擬合。
3、當類別太多時,錯誤可能就會增加的比較快。
4、在處理特征關聯性比較強的數據時表現得不是太好。
5、對於各類別樣本數量不一致的數據,在決策樹當中,信息增益的結果偏向於那些具有更多數值的特征。
2.17.5 熵的概念以及理解
熵:度量隨機變量的不確定性。
定義:假設隨機變量X的可能取值有$x_{1},x_{2},…,x_{n}$,對於每一個可能的取值$x_{i}$,其概率為$P(X=x_{i})=p_{i},i=1,2…,n$。隨機變量的熵為:
\(H(X)=-\sum_{i=1}^{n}p_{i}log_{2}p_{i}\)
對於樣本集合,假設樣本有k個類別,每個類別的概率為$\frac{|C_{k}|}{|D|}$,其中 ${|C_{k}|}{|D|}$為類別為k的樣本個數,$|D|$為樣本總數。樣本集合D的熵為:
\(H(D)=-\sum_{k=1}^{k}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|}\)
2.17.6 信息增益的理解
定義:以某特征劃分數據集前後的熵的差值。
熵可以表示樣本集合的不確定性,熵越大,樣本的不確定性就越大。因此可以使用劃分前後集合熵的差值來衡量使用當前特征對於樣本集合D劃分效果的好壞。 假設劃分前樣本集合D的熵為H(D)。使用某個特征A劃分數據集D,計算劃分後的數據子集的熵為H(D|A)。
則信息增益為:
\(g(D,A)=H(D)-H(D|A)\)
注:在決策樹構建的過程中我們總是希望集合往最快到達純度更高的子集合方向发展,因此我們總是選擇使得信息增益最大的特征來劃分當前數據集D。
思想:計算所有特征劃分數據集D,得到多個特征劃分數據集D的信息增益,從這些信息增益中選擇最大的,因而當前結點的劃分特征便是使信息增益最大的劃分所使用的特征。
另外這里提一下信息增益比相關知識:
$信息增益比=懲罰參數\times信息增益$
信息增益比本質:在信息增益的基礎之上乘上一個懲罰參數。特征個數較多時,懲罰參數較小;特征個數較少時,懲罰參數較大。
懲罰參數:數據集D以特征A作為隨機變量的熵的倒數。
2.17.7 剪枝處理的作用及策略
剪枝處理是決策樹學習算法用來解決過擬合問題的一種辦法。
在決策樹算法中,為了盡可能正確分類訓練樣本, 節點劃分過程不斷重覆, 有時候會造成決策樹分支過多,以至於將訓練樣本集自身特點當作泛化特點, 而導致過擬合。 因此可以采用剪枝處理來去掉一些分支來降低過擬合的風險。
剪枝的基本策略有預剪枝(pre-pruning)和後剪枝(post-pruning)。
預剪枝:在決策樹生成過程中,在每個節點劃分前先估計其劃分後的泛化性能, 如果不能提升,則停止劃分,將當前節點標記為葉結點。
後剪枝:生成決策樹以後,再自下而上對非葉結點進行考察, 若將此節點標記為葉結點可以帶來泛化性能提升,則修改之。
2.18 支持向量機
2.18.1 什麽是支持向量機
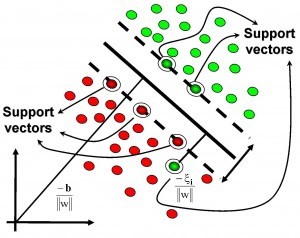
支持向量:在求解的過程中,會发現只根據部分數據就可以確定分類器,這些數據稱為支持向量。
支持向量機(Support Vector Machine,SVM):其含義是通過支持向量運算的分類器。
在一個二維環境中,其中點R,S,G點和其它靠近中間黑線的點可以看作為支持向量,它們可以決定分類器,即黑線的具體參數。
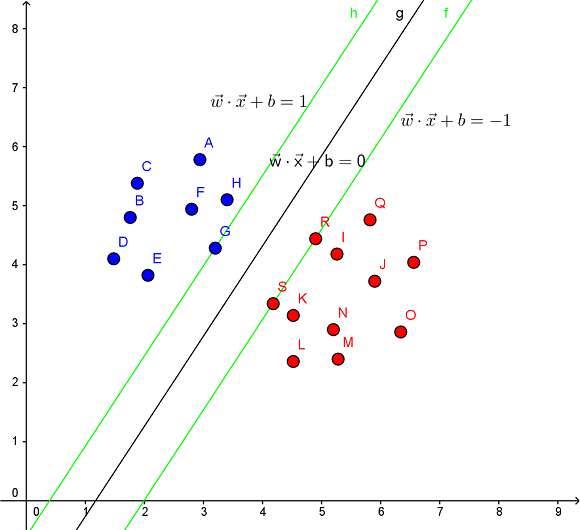
支持向量機是一種二分類模型,它的目的是尋找一個超平面來對樣本進行分割,分割的原則是邊界最大化,最終轉化為一個凸二次規劃問題來求解。由簡至繁的模型包括:
當訓練樣本線性可分時,通過硬邊界(hard margin)最大化,學習一個線性可分支持向量機;
當訓練樣本近似線性可分時,通過軟邊界(soft margin)最大化,學習一個線性支持向量機;
當訓練樣本線性不可分時,通過核技巧和軟邊界最大化,學習一個非線性支持向量機;
2.18.2 支持向量機能解決哪些問題
線性分類
在訓練數據中,每個數據都有n個的屬性和一個二分類類別標志,我們可以認為這些數據在一個n維空間里。我們的目標是找到一個n-1維的超平面,這個超平面可以將數據分成兩部分,每部分數據都屬於同一個類別。
這樣的超平面有很多,假如我們要找到一個最佳的超平面。此時,增加一個約束條件:要求這個超平面到每邊最近數據點的距離是最大的,成為最大邊距超平面。這個分類器即為最大邊距分類器。
非線性分類
SVM的一個優勢是支持非線性分類。它結合使用拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)條件,以及核函數可以生成非線性分類器。
2.18.3 核函數特點及其作用
引入核函數目的:把原坐標系里線性不可分的數據用核函數Kernel投影到另一個空間,盡量使得數據在新的空間里線性可分。
核函數方法的廣泛應用,與其特點是分不開的:
1)核函數的引入避免了“維數災難”,大大減小了計算量。而輸入空間的維數n對核函數矩陣無影響。因此,核函數方法可以有效處理高維輸入。
2)無需知道非線性變換函數Φ的形式和參數。
3)核函數的形式和參數的變化會隱式地改變從輸入空間到特征空間的映射,進而對特征空間的性質產生影響,最終改變各種核函數方法的性能。
4)核函數方法可以和不同的算法相結合,形成多種不同的基於核函數技術的方法,且這兩部分的設計可以單獨進行,並可以為不同的應用選擇不同的核函數和算法。
2.18.4 SVM為什麽引入對偶問題
1,對偶問題將原始問題中的約束轉為了對偶問題中的等式約束,對偶問題往往更加容易求解。
2,可以很自然的引用核函數(拉格朗日表達式里面有內積,而核函數也是通過內積進行映射的)。
3,在優化理論中,目標函數 f(x) 會有多種形式:如果目標函數和約束條件都為變量 x 的線性函數,稱該問題為線性規劃;如果目標函數為二次函數,約束條件為線性函數,稱該最優化問題為二次規劃;如果目標函數或者約束條件均為非線性函數,稱該最優化問題為非線性規劃。每個線性規劃問題都有一個與之對應的對偶問題,對偶問題有非常良好的性質,以下列舉幾個:
a, 對偶問題的對偶是原問題;
b, 無論原始問題是否是凸的,對偶問題都是凸優化問題;
c, 對偶問題可以給出原始問題一個下界;
d, 當滿足一定條件時,原始問題與對偶問題的解是完全等價的。
2.18.5 如何理解SVM中的對偶問題
在硬邊界支持向量機中,問題的求解可以轉化為凸二次規劃問題。
假設優化目標為 \(\begin{align} &\min_{\boldsymbol w, b}\frac{1}{2}||\boldsymbol w||^2\\ &s.t. y_i(\boldsymbol w^T\boldsymbol x_i+b)\geqslant 1, i=1,2,\cdots,m.\\ \end{align} \tag{1}\) step 1. 轉化問題: \(\min_{\boldsymbol w, b} \max_{\alpha_i \geqslant 0} \left\{\frac{1}{2}||\boldsymbol w||^2 + \sum_{i=1}^m\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))\right\} \tag{2}\) 上式等價於原問題,因為若滿足(1)中不等式約束,則(2)式求max時,$\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))$必須取0,與(1)等價;若不滿足(1)中不等式約束,(2)中求max會得到無窮大。 交換min和max獲得其對偶問題: \(\max_{\alpha_i \geqslant 0} \min_{\boldsymbol w, b} \left\{\frac{1}{2}||\boldsymbol w||^2 + \sum_{i=1}^m\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))\right\}\) 交換之後的對偶問題和原問題並不相等,上式的解小於等於原問題的解。
step 2.現在的問題是如何找到問題(1) 的最優值的一個最好的下界? \(\frac{1}{2}||\boldsymbol w||^2 < v\\ 1 - y_i(\boldsymbol w^T\boldsymbol x_i+b) \leqslant 0\tag{3}\) 若方程組(3)無解, 則v是問題(1)的一個下界。若(3)有解, 則 \(\forall \boldsymbol \alpha > 0 , \ \min_{\boldsymbol w, b} \left\{\frac{1}{2}||\boldsymbol w||^2 + \sum_{i=1}^m\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))\right\} < v\) 由逆否命題得:若 \(\exists \boldsymbol \alpha > 0 , \ \min_{\boldsymbol w, b} \left\{\frac{1}{2}||\boldsymbol w||^2 + \sum_{i=1}^m\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))\right\} \geqslant v\) 則(3)無解。
那麽v是問題
(1)的一個下界。 要求得一個好的下界,取最大值即可 \(\max_{\alpha_i \geqslant 0} \min_{\boldsymbol w, b} \left\{\frac{1}{2}||\boldsymbol w||^2 + \sum_{i=1}^m\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))\right\}\) step 3. 令 \(L(\boldsymbol w, b,\boldsymbol a) = \frac{1}{2}||\boldsymbol w||^2 + \sum_{i=1}^m\alpha_i(1 - y_i(\boldsymbol w^T\boldsymbol x_i+b))\) $p^$為原問題的最小值,對應的$w,b$分別為$w^,b^*$,則對於任意的$a>0$:
\[p^*=\frac{1}{2}||\boldsymbol w^*||^2 \geqslant L(\boldsymbol w^*, b,\boldsymbol a) \geqslant \min_{\boldsymbol w, b} L(\boldsymbol w, b,\boldsymbol a)\]則 \(\min_{\boldsymbol w, b}L(\boldsymbol w, b,\boldsymbol a)\)是問題(1)的一個下界。
此時,取最大值即可求得好的下界,即 \(\max_{\alpha_i \geqslant 0} \min_{\boldsymbol w, b} L(\boldsymbol w, b,\boldsymbol a)\)
2.18.7 常見的核函數有哪些
| 核函數 | 表達式 | 備注 |
|---|---|---|
| Linear Kernel線性核 | $k(x,y)=x^{t}y+c$ | |
| Polynomial Kernel多項式核 | $k(x,y)=(ax^{t}y+c)^{d}$ | $d\geqslant1$為多項式的次數 |
| Exponential Kernel指數核 | $k(x,y)=exp(-\frac{\left |x-y \right |}{2\sigma ^{2}})$ | $\sigma>0$ |
| Gaussian Kernel高斯核 | $k(x,y)=exp(-\frac{\left |x-y \right |^{2}}{2\sigma ^{2}})$ | $\sigma$為高斯核的帶寬,$\sigma>0$, |
| Laplacian Kernel拉普拉斯核 | $k(x,y)=exp(-\frac{\left |x-y \right |}{\sigma})$ | $\sigma>0$ |
| ANOVA Kernel | $k(x,y)=exp(-\sigma(x^{k}-y^{k})^{2})^{d}$ | |
| Sigmoid Kernel | $k(x,y)=tanh(ax^{t}y+c)$ | $tanh$為雙曲正切函數,$a>0,c<0$ |
2.18.9 SVM主要特點
特點:
(1) SVM方法的理論基礎是非線性映射,SVM利用內積核函數代替向高維空間的非線性映射。
(2) SVM的目標是對特征空間劃分得到最優超平面,SVM方法核心是最大化分類邊界。
(3) 支持向量是SVM的訓練結果,在SVM分類決策中起決定作用的是支持向量。
(4) SVM是一種有堅實理論基礎的新穎的適用小樣本學習方法。它基本上不涉及概率測度及大數定律等,也簡化了通常的分類和回歸等問題。
(5) SVM的最終決策函數只由少數的支持向量所確定,計算的覆雜性取決於支持向量的數目,而不是樣本空間的維數,這在某種意義上避免了“維數災難”。
(6) 少數支持向量決定了最終結果,這不但可以幫助我們抓住關鍵樣本、“剔除”大量冗余樣本,而且注定了該方法不但算法簡單,而且具有較好的“魯棒性”。這種魯棒性主要體現在:
①增、刪非支持向量樣本對模型沒有影響;
②支持向量樣本集具有一定的魯棒性;
③有些成功的應用中,SVM方法對核的選取不敏感
(7) SVM學習問題可以表示為凸優化問題,因此可以利用已知的有效算法发現目標函數的全局最小值。而其他分類方法(如基於規則的分類器和人工神經網絡)都采用一種基於貪心學習的策略來搜索假設空間,這種方法一般只能獲得局部最優解。
(8) SVM通過最大化決策邊界的邊緣來控制模型的能力。盡管如此,用戶必須提供其他參數,如使用核函數類型和引入松弛變量等。
(9) SVM在小樣本訓練集上能夠得到比其它算法好很多的結果。SVM優化目標是結構化風險最小,而不是經驗風險最小,避免了過擬合問題,通過margin的概念,得到對數據分布的結構化描述,減低了對數據規模和數據分布的要求,有優秀的泛化能力。
(10) 它是一個凸優化問題,因此局部最優解一定是全局最優解的優點。
2.18.10 SVM主要缺點
(1) SVM算法對大規模訓練樣本難以實施
SVM的空間消耗主要是存儲訓練樣本和核矩陣,由於SVM是借助二次規劃來求解支持向量,而求解二次規劃將涉及m階矩陣的計算(m為樣本的個數),當m數目很大時該矩陣的存儲和計算將耗費大量的機器內存和運算時間。
如果數據量很大,SVM的訓練時間就會比較長,如垃圾郵件的分類檢測,沒有使用SVM分類器,而是使用簡單的樸素貝葉斯分類器,或者是使用邏輯回歸模型分類。
(2) 用SVM解決多分類問題存在困難
經典的支持向量機算法只給出了二類分類的算法,而在實際應用中,一般要解決多類的分類問題。可以通過多個二類支持向量機的組合來解決。主要有一對多組合模式、一對一組合模式和SVM決策樹;再就是通過構造多個分類器的組合來解決。主要原理是克服SVM固有的缺點,結合其他算法的優勢,解決多類問題的分類精度。如:與粗糙集理論結合,形成一種優勢互補的多類問題的組合分類器。
(3) 對缺失數據敏感,對參數和核函數的選擇敏感
支持向量機性能的優劣主要取決於核函數的選取,所以對於一個實際問題而言,如何根據實際的數據模型選擇合適的核函數從而構造SVM算法。目前比較成熟的核函數及其參數的選擇都是人為的,根據經驗來選取的,帶有一定的隨意性。在不同的問題領域,核函數應當具有不同的形式和參數,所以在選取時候應該將領域知識引入進來,但是目前還沒有好的方法來解決核函數的選取問題。
2.18.11 邏輯回歸與SVM的異同
相同點:
- LR和SVM都是分類算法。
- LR和SVM都是監督學習算法。
- LR和SVM都是判別模型。
- 如果不考慮核函數,LR和SVM都是線性分類算法,也就是說他們的分類決策面都是線性的。 說明:LR也是可以用核函數的.但LR通常不采用核函數的方法。(計算量太大)
不同點:
1、LR采用log損失,SVM采用合頁(hinge)損失。
邏輯回歸的損失函數:
\(J(\theta)=-\frac{1}{m}\sum^m_{i=1}\left[y^{i}logh_{\theta}(x^{i})+ (1-y^{i})log(1-h_{\theta}(x^{i}))\right]\)
支持向量機的目標函數:
\(L(w,n,a)=\frac{1}{2}||w||^2-\sum^n_{i=1}\alpha_i \left( y_i(w^Tx_i+b)-1\right)\)
邏輯回歸方法基於概率理論,假設樣本為1的概率可以用sigmoid函數來表示,然後通過極大似然估計的方法估計出參數的值。
支持向量機基於幾何邊界最大化原理,認為存在最大幾何邊界的分類面為最優分類面。
2、LR對異常值敏感,SVM對異常值不敏感。
支持向量機只考慮局部的邊界線附近的點,而邏輯回歸考慮全局。LR模型找到的那個超平面,是盡量讓所有點都遠離他,而SVM尋找的那個超平面,是只讓最靠近中間分割線的那些點盡量遠離,即只用到那些支持向量的樣本。
支持向量機改變非支持向量樣本並不會引起決策面的變化。
邏輯回歸中改變任何樣本都會引起決策面的變化。
3、計算覆雜度不同。對於海量數據,SVM的效率較低,LR效率比較高
當樣本較少,特征維數較低時,SVM和LR的運行時間均比較短,SVM較短一些。準確率的話,LR明顯比SVM要高。當樣本稍微增加些時,SVM運行時間開始增長,但是準確率趕超了LR。SVM時間雖長,但在可接受範圍內。當數據量增長到20000時,特征維數增長到200時,SVM的運行時間劇烈增加,遠遠超過了LR的運行時間。但是準確率卻和LR相差無幾。(這其中主要原因是大量非支持向量參與計算,造成SVM的二次規劃問題)
4、對非線性問題的處理方式不同
LR主要靠特征構造,必須組合交叉特征,特征離散化。SVM也可以這樣,還可以通過核函數kernel(因為只有支持向量參與核計算,計算覆雜度不高)。由於可以利用核函數,SVM則可以通過對偶求解高效處理。LR則在特征空間維度很高時,表現較差。
5、SVM的損失函數就自帶正則。
損失函數中的1/2||w||^2項,這就是為什麽SVM是結構風險最小化算法的原因!!!而LR必須另外在損失函數上添加正則項!!!
6、SVM自帶結構風險最小化,LR則是經驗風險最小化。
7、SVM會用核函數而LR一般不用核函數。
2.19 貝葉斯分類器
2.19.1 圖解極大似然估計
極大似然估計的原理,用一張圖片來說明,如下圖所示:
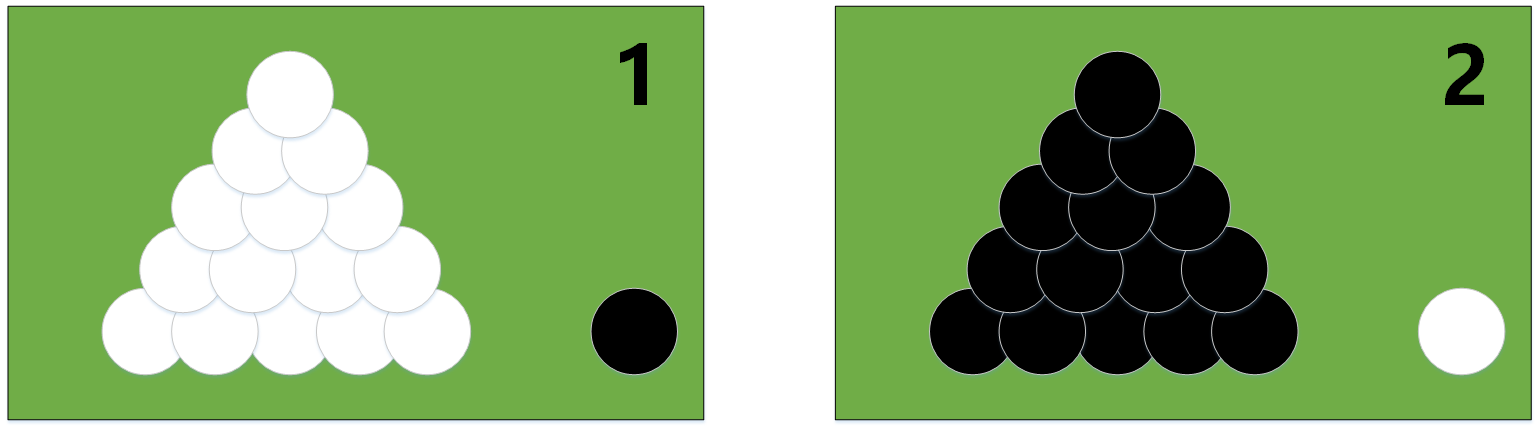
例:有兩個外形完全相同的箱子,1號箱有99只白球,1只黑球;2號箱有1只白球,99只黑球。在一次實驗中,取出的是黑球,請問是從哪個箱子中取出的?
一般的根據經驗想法,會猜測這只黑球最像是從2號箱取出,此時描述的“最像”就有“最大似然”的意思,這種想法常稱為“最大似然原理”。
2.19.2 極大似然估計原理
總結起來,最大似然估計的目的就是:利用已知的樣本結果,反推最有可能(最大概率)導致這樣結果的參數值。
極大似然估計是建立在極大似然原理的基礎上的一個統計方法。極大似然估計提供了一種給定觀察數據來評估模型參數的方法,即:“模型已定,參數未知”。通過若幹次試驗,觀察其結果,利用試驗結果得到某個參數值能夠使樣本出現的概率為最大,則稱為極大似然估計。
由於樣本集中的樣本都是獨立同分布,可以只考慮一類樣本集$D$,來估計參數向量$\vec\theta$。記已知的樣本集為: \(D=\vec x_{1},\vec x_{2},...,\vec x_{n}\) 似然函數(likelihood function):聯合概率密度函數$p(D|\vec\theta )$稱為相對於$\vec x_{1},\vec x_{2},…,\vec x_{n}$的$\vec\theta$的似然函數。 \(l(\vec\theta )=p(D|\vec\theta ) =p(\vec x_{1},\vec x_{2},...,\vec x_{n}|\vec\theta )=\prod_{i=1}^{n}p(\vec x_{i}|\vec \theta )\) 如果$\hat{\vec\theta}$是參數空間中能使似然函數$l(\vec\theta)$最大的$\vec\theta$值,則$\hat{\vec\theta}$應該是“最可能”的參數值,那麽$\hat{\vec\theta}$就是$\theta$的極大似然估計量。它是樣本集的函數,記作: \(\hat{\vec\theta}=d(D)= \mathop {\arg \max}_{\vec\theta} l(\vec\theta )\) $\hat{\vec\theta}(\vec x_{1},\vec x_{2},…,\vec x_{n})$稱為極大似然函數估計值。
2.19.3 貝葉斯分類器基本原理
貝葉斯決策論通過相關概率已知的情況下利用誤判損失來選擇最優的類別分類。
假設有$N$種可能的分類標記,記為$Y={c_1,c_2,…,c_N}$,那對於樣本$\boldsymbol{x}$,它屬於哪一類呢?
計算步驟如下:
step 1. 算出樣本$\boldsymbol{x}$屬於第i個類的概率,即$P(c_i|x)$;
step 2. 通過比較所有的$P(c_i|\boldsymbol{x})$,得到樣本$\boldsymbol{x}$所屬的最佳類別。
step 3. 將類別$c_i$和樣本$\boldsymbol{x}$代入到貝葉斯公式中,得到:
\(P(c_i|\boldsymbol{x})=\frac{P(\boldsymbol{x}|c_i)P(c_i)}{P(\boldsymbol{x})}.\)
一般來說,$P(c_i)$為先驗概率,$P(\boldsymbol{x}|c_i)$為條件概率,$P(\boldsymbol{x})$是用於歸一化的證據因子。對於$P(c_i)$可以通過訓練樣本中類別為$c_i$的樣本所占的比例進行估計;此外,由於只需要找出最大的$P(\boldsymbol{x}|c_i)$,因此我們並不需要計算$P(\boldsymbol{x})$。
為了求解條件概率,基於不同假設提出了不同的方法,以下將介紹樸素貝葉斯分類器和半樸素貝葉斯分類器。
2.19.4 樸素貝葉斯分類器
假設樣本$\boldsymbol{x}$包含$d$個屬性,即$\boldsymbol{x}={ x_1,x_2,…,x_d}$。於是有: \(P(\boldsymbol{x}|c_i)=P(x_1,x_2,\cdots,x_d|c_i)\) 這個聯合概率難以從有限的訓練樣本中直接估計得到。於是,樸素貝葉斯(Naive Bayesian,簡稱NB)采用了“屬性條件獨立性假設”:對已知類別,假設所有屬性相互獨立。於是有: \(P(x_1,x_2,\cdots,x_d|c_i)=\prod_{j=1}^d P(x_j|c_i)\) 這樣的話,我們就可以很容易地推出相應的判定準則了: \(h_{nb}(\boldsymbol{x})=\mathop{\arg \max}_{c_i\in Y} P(c_i)\prod_{j=1}^dP(x_j|c_i)\) 條件概率$P(x_j|c_i)$的求解
如果$x_j$是標簽屬性,那麽我們可以通過計數的方法估計$P(x_j|c_i)$ \(P(x_j|c_i)=\frac{P(x_j,c_i)}{P(c_i)}\approx\frac{\#(x_j,c_i)}{\#(c_i)}\) 其中,$#(x_j,c_i)$表示在訓練樣本中$x_j$與$c_{i}$共同出現的次數。
如果$x_j$是數值屬性,通常我們假設類別中$c_{i}$的所有樣本第$j$個屬性的值服從正態分布。我們首先估計這個分布的均值$μ$和方差$σ$,然後計算$x_j$在這個分布中的概率密度$P(x_j|c_i)$。
2.19.5 舉例理解樸素貝葉斯分類器
使用經典的西瓜訓練集如下:
| 編號 | 色澤 | 根蒂 | 敲聲 | 紋理 | 臍部 | 觸感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 青綠 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | 是 |
| 2 | 烏黑 | 蜷縮 | 沈悶 | 清晰 | 凹陷 | 硬滑 | 0.774 | 0.376 | 是 |
| 3 | 烏黑 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 0.634 | 0.264 | 是 |
| 4 | 青綠 | 蜷縮 | 沈悶 | 清晰 | 凹陷 | 硬滑 | 0.608 | 0.318 | 是 |
| 5 | 淺白 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 0.556 | 0.215 | 是 |
| 6 | 青綠 | 稍蜷 | 濁響 | 清晰 | 稍凹 | 軟粘 | 0.403 | 0.237 | 是 |
| 7 | 烏黑 | 稍蜷 | 濁響 | 稍糊 | 稍凹 | 軟粘 | 0.481 | 0.149 | 是 |
| 8 | 烏黑 | 稍蜷 | 濁響 | 清晰 | 稍凹 | 硬滑 | 0.437 | 0.211 | 是 |
| 9 | 烏黑 | 稍蜷 | 沈悶 | 稍糊 | 稍凹 | 硬滑 | 0.666 | 0.091 | 否 |
| 10 | 青綠 | 硬挺 | 清脆 | 清晰 | 平坦 | 軟粘 | 0.243 | 0.267 | 否 |
| 11 | 淺白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 0.245 | 0.057 | 否 |
| 12 | 淺白 | 蜷縮 | 濁響 | 模糊 | 平坦 | 軟粘 | 0.343 | 0.099 | 否 |
| 13 | 青綠 | 稍蜷 | 濁響 | 稍糊 | 凹陷 | 硬滑 | 0.639 | 0.161 | 否 |
| 14 | 淺白 | 稍蜷 | 沈悶 | 稍糊 | 凹陷 | 硬滑 | 0.657 | 0.198 | 否 |
| 15 | 烏黑 | 稍蜷 | 濁響 | 清晰 | 稍凹 | 軟粘 | 0.360 | 0.370 | 否 |
| 16 | 淺白 | 蜷縮 | 濁響 | 模糊 | 平坦 | 硬滑 | 0.593 | 0.042 | 否 |
| 17 | 青綠 | 蜷縮 | 沈悶 | 稍糊 | 稍凹 | 硬滑 | 0.719 | 0.103 | 否 |
對下面的測試例“測1”進行 分類:
| 編號 | 色澤 | 根蒂 | 敲聲 | 紋理 | 臍部 | 觸感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 測1 | 青綠 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | ? |
首先,估計類先驗概率$P(c_j)$,有 \(\begin{align} &P(好瓜=是)=\frac{8}{17}=0.471 \newline &P(好瓜=否)=\frac{9}{17}=0.529 \end{align}\) 然後,為每個屬性估計條件概率(這里,對於連續屬性,假定它們服從正態分布) \(P_{青綠|是}=P(色澤=青綠|好瓜=是)=\frac{3}{8}=0.375\)
\[P_{青綠|否}=P(色澤=青綠|好瓜=否)=\frac{3}{9}\approx0.333\] \[P_{蜷縮|是}=P(根蒂=蜷縮|好瓜=是)=\frac{5}{8}=0.625\] \[P_{蜷縮|否}=P(根蒂=蜷縮|好瓜=否)=\frac{3}{9}=0.333\] \[P_{濁響|是}=P(敲聲=濁響|好瓜=是)=\frac{6}{8}=0.750\] \[P_{濁響|否}=P(敲聲=濁響|好瓜=否)=\frac{4}{9}\approx 0.444\] \[P_{清晰|是}=P(紋理=清晰|好瓜=是)=\frac{7}{8}= 0.875\] \[P_{清晰|否}=P(紋理=清晰|好瓜=否)=\frac{2}{9}\approx 0.222\] \[P_{凹陷|是}=P(臍部=凹陷|好瓜=是)=\frac{6}{8}= 0.750\] \[P_{凹陷|否}=P(臍部=凹陷|好瓜=否)=\frac{2}{9} \approx 0.222\] \[P_{硬滑|是}=P(觸感=硬滑|好瓜=是)=\frac{6}{8}= 0.750\] \[P_{硬滑|否}=P(觸感=硬滑|好瓜=否)=\frac{6}{9} \approx 0.667\] \[\begin{aligned} \rho_{密度:0.697|是}&=\rho(密度=0.697|好瓜=是)\\&=\frac{1}{\sqrt{2 \pi}\times0.129}exp\left( -\frac{(0.697-0.574)^2}{2\times0.129^2}\right) \approx 1.959 \end{aligned}\] \[\begin{aligned} \rho_{密度:0.697|否}&=\rho(密度=0.697|好瓜=否)\\&=\frac{1}{\sqrt{2 \pi}\times0.195}exp\left( -\frac{(0.697-0.496)^2}{2\times0.195^2}\right) \approx 1.203 \end{aligned}\] \[\begin{aligned} \rho_{含糖:0.460|是}&=\rho(密度=0.460|好瓜=是)\\&=\frac{1}{\sqrt{2 \pi}\times0.101}exp\left( -\frac{(0.460-0.279)^2}{2\times0.101^2}\right) \approx 0.788 \end{aligned}\] \[\begin{aligned} \rho_{含糖:0.460|否}&=\rho(密度=0.460|好瓜=是)\\&=\frac{1}{\sqrt{2 \pi}\times0.108}exp\left( -\frac{(0.460-0.154)^2}{2\times0.108^2}\right) \approx 0.066 \end{aligned}\]於是有 \(\begin{align} P(&好瓜=是)\times P_{青綠|是} \times P_{蜷縮|是} \times P_{濁響|是} \times P_{清晰|是} \times P_{凹陷|是}\newline &\times P_{硬滑|是} \times p_{密度:0.697|是} \times p_{含糖:0.460|是} \approx 0.063 \newline\newline P(&好瓜=否)\times P_{青綠|否} \times P_{蜷縮|否} \times P_{濁響|否} \times P_{清晰|否} \times P_{凹陷|否}\newline &\times P_{硬滑|否} \times p_{密度:0.697|否} \times p_{含糖:0.460|否} \approx 6.80\times 10^{-5} \end{align}\)
由於$0.063>6.80\times 10^{-5}$,因此,樸素貝葉斯分類器將測試樣本“測1”判別為“好瓜”。
2.19.6 半樸素貝葉斯分類器
樸素貝葉斯采用了“屬性條件獨立性假設”,半樸素貝葉斯分類器的基本想法是適當考慮一部分屬性間的相互依賴信息。獨依賴估計(One-Dependence Estimator,簡稱ODE)是半樸素貝葉斯分類器最常用的一種策略。顧名思義,獨依賴是假設每個屬性在類別之外最多依賴一個其他屬性,即: \(P(\boldsymbol{x}|c_i)=\prod_{j=1}^d P(x_j|c_i,{\rm pa}_j)\) 其中$pa_j$為屬性$x_i$所依賴的屬性,成為$x_i$的父屬性。假設父屬性$pa_j$已知,那麽可以使用下面的公式估計$P(x_j|c_i,{\rm pa}_j)$ \(P(x_j|c_i,{\rm pa}_j)=\frac{P(x_j,c_i,{\rm pa}_j)}{P(c_i,{\rm pa}_j)}\)
2.20 EM算法
2.20.1 EM算法基本思想
最大期望算法(Expectation-Maximization algorithm, EM),是一類通過叠代進行極大似然估計的優化算法,通常作為牛頓叠代法的替代,用於對包含隱變量或缺失數據的概率模型進行參數估計。
最大期望算法基本思想是經過兩個步驟交替進行計算:
第一步是計算期望(E),利用對隱藏變量的現有估計值,計算其最大似然估計值;
第二步是最大化(M),最大化在E步上求得的最大似然值來計算參數的值。
M步上找到的參數估計值被用於下一個E步計算中,這個過程不斷交替進行。
2.20.2 EM算法推導
對於$m$個樣本觀察數據$x=(x^{1},x^{2},…,x^{m})$,現在想找出樣本的模型參數$\theta$,其極大化模型分布的對數似然函數為: \(\theta = \mathop{\arg\max}_\theta\sum\limits_{i=1}^m logP(x^{(i)};\theta)\) 如果得到的觀察數據有未觀察到的隱含數據$z=(z^{(1)},z^{(2)},…z^{(m)})$,極大化模型分布的對數似然函數則為: \(\theta =\mathop{\arg\max}_\theta\sum\limits_{i=1}^m logP(x^{(i)};\theta) = \mathop{\arg\max}_\theta\sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}P(x^{(i)}, z^{(i)};\theta) \tag{a}\) 由於上式不能直接求出$\theta$,采用縮放技巧: \(\begin{align} \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}P(x^{(i)}, z^{(i)};\theta) & = \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}Q_i(z^{(i)})\frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})} \\ & \geqslant \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})} \end{align} \tag{1}\) 上式用到了Jensen不等式: \(log\sum\limits_j\lambda_jy_j \geqslant \sum\limits_j\lambda_jlogy_j\;\;, \lambda_j \geqslant 0, \sum\limits_j\lambda_j =1\) 並且引入了一個未知的新分布$Q_i(z^{(i)})$。
此時,如果需要滿足Jensen不等式中的等號,所以有: \(\frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})} =c, c為常數\) 由於$Q_i(z^{(i)})$是一個分布,所以滿足 \(\sum\limits_{z}Q_i(z^{(i)}) =1\) 綜上,可得: \(Q_i(z^{(i)}) = \frac{P(x^{(i)}, z^{(i)};\theta)}{\sum\limits_{z}P(x^{(i)}, z^{(i)};\theta)} = \frac{P(x^{(i)}, z^{(i)};\theta)}{P(x^{(i)};\theta)} = P( z^{(i)}|x^{(i)};\theta)\) 如果$Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)};\theta)$ ,則第(1)式是我們的包含隱藏數據的對數似然的一個下界。如果我們能極大化這個下界,則也在嘗試極大化我們的對數似然。即我們需要最大化下式: \(\mathop{\arg\max}_\theta \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})}\) 簡化得: \(\mathop{\arg\max}_\theta \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)}, z^{(i)};\theta)}\) 以上即為EM算法的M步,$\sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)}, z^{(i)};\theta)}$可理解為$logP(x^{(i)}, z^{(i)};\theta) $基於條件概率分布$Q_i(z^{(i)}) $的期望。以上即為EM算法中E步和M步的具體數學含義。
2.20.3 圖解EM算法
考慮上一節中的(a)式,表達式中存在隱變量,直接找到參數估計比較困難,通過EM算法叠代求解下界的最大值到收斂為止。
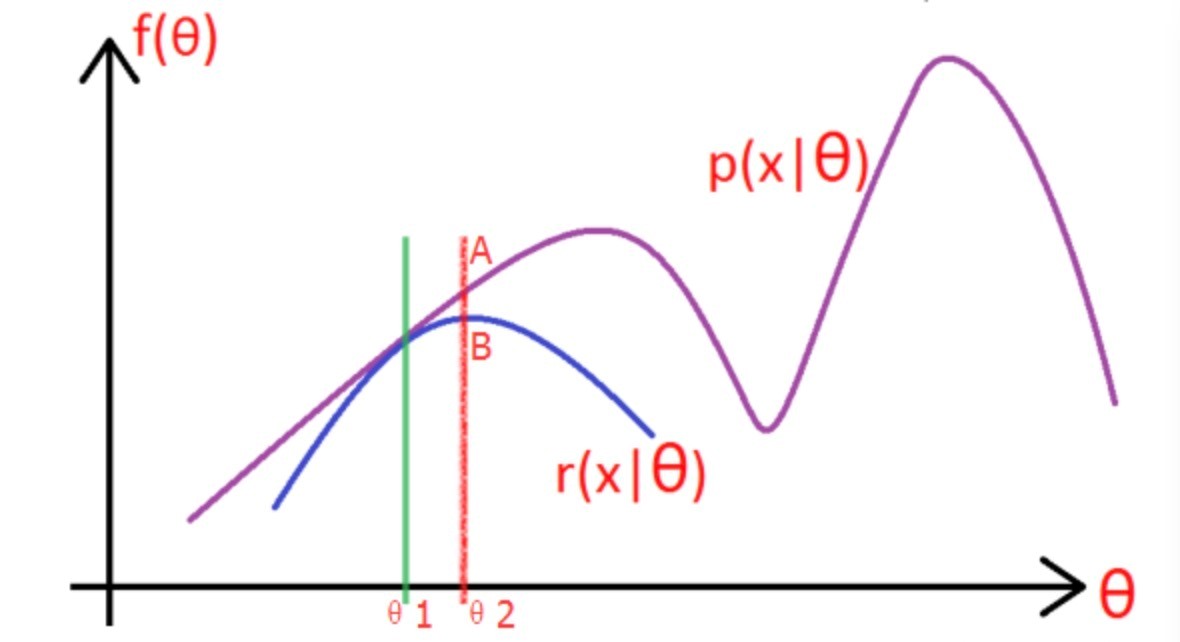
圖片中的紫色部分是我們的目標模型$p(x|\theta)$,該模型覆雜,難以求解析解,為了消除隱變量$z^{(i)}$的影響,我們可以選擇一個不包含$z^{(i)}$的模型$r(x|\theta)$,使其滿足條件$r(x|\theta) \leqslant p(x|\theta) $。
求解步驟如下:
(1)選取 $\theta_1$,使得 $r(x|\theta_1) = p(x|\theta_1)$,然後對此時的 $r$ 求取最大值,得到極值點 $\theta_2$,實現參數的更新。
(2)重覆以上過程到收斂為止,在更新過程中始終滿足$r \leqslant p $.
2.20.4 EM算法流程
輸入:觀察數據$x=(x^{(1)},x^{(2)},…x^{(m)})$,聯合分布$p(x,z ;\theta)$,條件分布$p(z|x; \theta)$,最大叠代次數$J$
1)隨機初始化模型參數 $\theta$的初值 $\theta^0$。
2)$for \ j \ from \ 1 \ to \ j$:
a) E步。計算聯合分布的條件概率期望: \(Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)}, \theta^{j})\)
\[L(\theta, \theta^{j}) = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)}, \theta^{j})log{P(x^{(i)}, z^{(i)};\theta)}\] b) M步。極大化$L(\theta, \theta^{j})$,得到$\theta^{j+1}$: \(\theta^{j+1} = \mathop{\arg\max}_\theta L(\theta, \theta^{j})\) c) 如果$\theta^{j+1}$收斂,則算法結束。否則繼續回到步驟a)進行E步叠代。
輸出:模型參數$\theta$。
2.21 降維和聚類
2.21.1 圖解為什麽會產生維數災難
假如數據集包含10張照片,照片中包含三角形和圓兩種形狀。現在來設計一個分類器進行訓練,讓這個分類器對其他的照片進行正確分類(假設三角形和圓的總數是無限大),簡單的,我們用一個特征進行分類:

圖2.21.1.a
從上圖可看到,如果僅僅只有一個特征進行分類,三角形和圓幾乎是均勻分布在這條線段上,很難將10張照片線性分類。那麽,增加一個特征後的情況會怎麽樣:
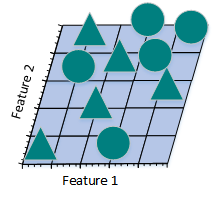
圖2.21.1.b
增加一個特征後,我們发現仍然無法找到一條直線將貓和狗分開。所以,考慮需要再增加一個特征:
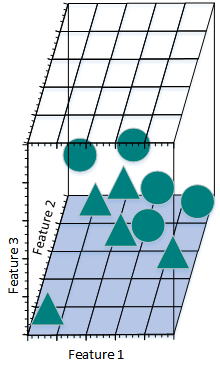
圖2.21.1.c
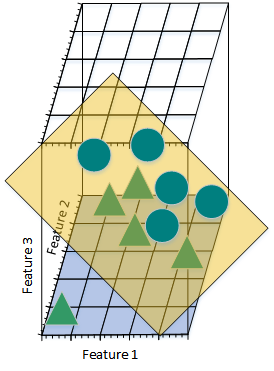
圖2.21.1.d
此時,可以找到一個平面將三角形和圓分開。
現在計算一下不同特征數是樣本的密度:
(1)一個特征時,假設特征空間時長度為5的線段,則樣本密度為$10 \div 5 = 2$。
(2)兩個特征時,特征空間大小為$ 5\times5 = 25$,樣本密度為$10 \div 25 = 0.4$。
(3)三個特征時,特征空間大小是$ 5\times5\times5 = 125$,樣本密度為$10 \div 125 = 0.08$。
以此類推,如果繼續增加特征數量,樣本密度會越來越稀疏,此時,更容易找到一個超平面將訓練樣本分開。當特征數量增長至無限大時,樣本密度就變得非常稀疏。
下面看一下將高維空間的分類結果映射到低維空間時,會出現什麽情況?
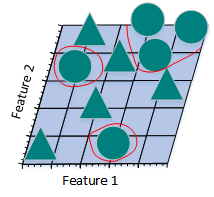
圖2.21.1.e
上圖是將三維特征空間映射到二維特征空間後的結果。盡管在高維特征空間時訓練樣本線性可分,但是映射到低維空間後,結果正好相反。事實上,增加特征數量使得高維空間線性可分,相當於在低維空間內訓練一個覆雜的非線性分類器。不過,這個非線性分類器太過“聰明”,僅僅學到了一些特例。如果將其用來辨別那些未曾出現在訓練樣本中的測試樣本時,通常結果不太理想,會造成過擬合問題。
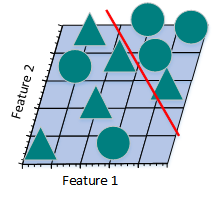
圖2.21.1.f
上圖所示的只采用2個特征的線性分類器分錯了一些訓練樣本,準確率似乎沒有圖2.21.1.e的高,但是,采用2個特征的線性分類器的泛化能力比采用3個特征的線性分類器要強。因為,采用2個特征的線性分類器學習到的不只是特例,而是一個整體趨勢,對於那些未曾出現過的樣本也可以比較好地辨別開來。換句話說,通過減少特征數量,可以避免出現過擬合問題,從而避免“維數災難”。
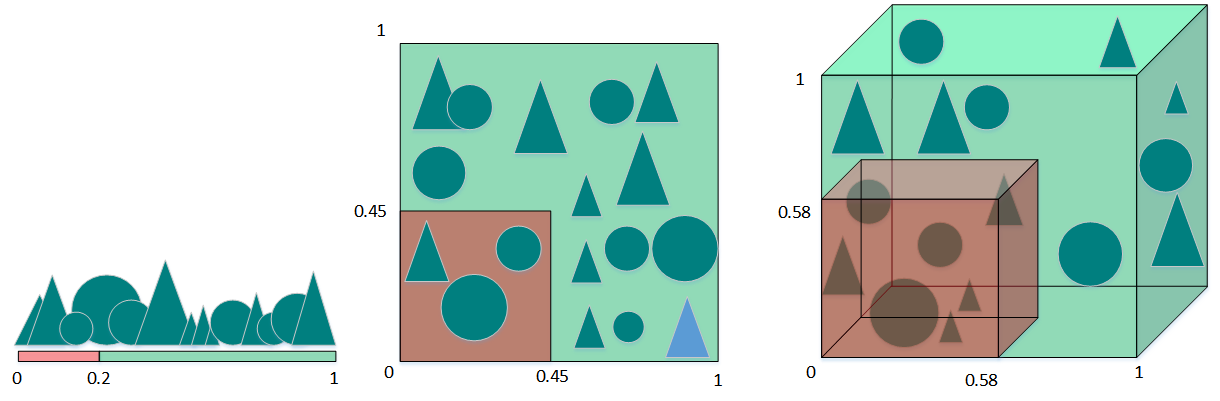
上圖從另一個角度詮釋了“維數災難”。假設只有一個特征時,特征的值域是0到1,每一個三角形和圓的特征值都是唯一的。如果我們希望訓練樣本覆蓋特征值值域的20%,那麽就需要三角形和圓總數的20%。我們增加一個特征後,為了繼續覆蓋特征值值域的20%就需要三角形和圓總數的45%($0.452^2\approx0.2$)。繼續增加一個特征後,需要三角形和圓總數的58%($0.583^3\approx0.2$)。隨著特征數量的增加,為了覆蓋特征值值域的20%,就需要更多的訓練樣本。如果沒有足夠的訓練樣本,就可能會出現過擬合問題。
通過上述例子,我們可以看到特征數量越多,訓練樣本就會越稀疏,分類器的參數估計就會越不準確,更加容易出現過擬合問題。“維數災難”的另一個影響是訓練樣本的稀疏性並不是均勻分布的。處於中心位置的訓練樣本比四周的訓練樣本更加稀疏。

假設有一個二維特征空間,如上圖所示的矩形,在矩形內部有一個內切的圓形。由於越接近圓心的樣本越稀疏,因此,相比於圓形內的樣本,那些位於矩形四角的樣本更加難以分類。當維數變大時,特征超空間的容量不變,但單位圓的容量會趨於0,在高維空間中,大多數訓練數據駐留在特征超空間的角落。散落在角落的數據要比處於中心的數據難於分類。
2.21.2 怎樣避免維數災難
有待完善!!!
解決維度災難問題:
主成分分析法PCA,線性判別法LDA
奇異值分解簡化數據、拉普拉斯特征映射
Lassio縮減系數法、小波分析法、
2.21.3 聚類和降維有什麽區別與聯系
聚類用於找尋數據內在的分布結構,既可以作為一個單獨的過程,比如異常檢測等等。也可作為分類等其他學習任務的前驅過程。聚類是標準的無監督學習。
1)在一些推薦系統中需確定新用戶的類型,但定義“用戶類型”卻可能不太容易,此時往往可先對原有的用戶數據進行聚類,根據聚類結果將每個簇定義為一個類,然後再基於這些類訓練分類模型,用於判別新用戶的類型。
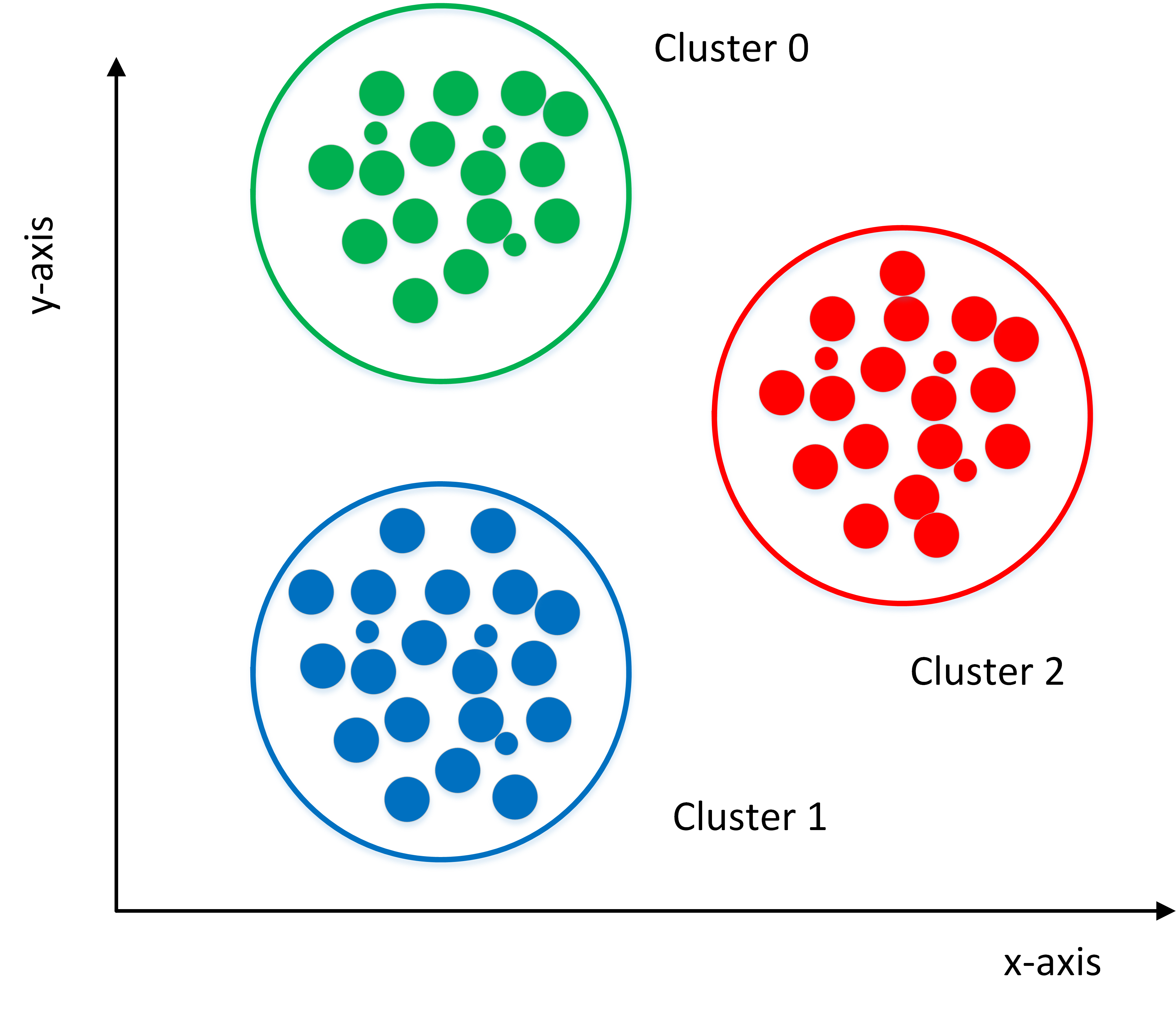
2)而降維則是為了緩解維數災難的一個重要方法,就是通過某種數學變換將原始高維屬性空間轉變為一個低維“子空間”。其基於的假設就是,雖然人們平時觀測到的數據樣本雖然是高維的,但是實際上真正與學習任務相關的是個低維度的分布。從而通過最主要的幾個特征維度就可以實現對數據的描述,對於後續的分類很有幫助。比如對於Kaggle(數據分析競賽平台之一)上的泰坦尼克號生還問題。通過給定一個乘客的許多特征如年齡、姓名、性別、票價等,來判斷其是否能在海難中生還。這就需要首先進行特征篩選,從而能夠找出主要的特征,讓學習到的模型有更好的泛化性。
聚類和降維都可以作為分類等問題的預處理步驟。
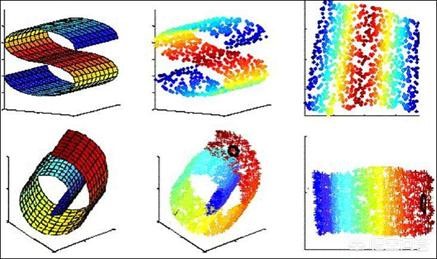
但是他們雖然都能實現對數據的約減。但是二者適用的對象不同,聚類針對的是數據點,而降維則是對於數據的特征。另外它們有著很多種實現方法。聚類中常用的有K-means、層次聚類、基於密度的聚類等;降維中常用的則PCA、Isomap、LLE等。
2.21.4 有哪些聚類算法優劣衡量標準
不同聚類算法有不同的優劣和不同的適用條件。可從以下方面進行衡量判斷: 1、算法的處理能力:處理大的數據集的能力,即算法覆雜度;處理數據噪聲的能力;處理任意形狀,包括有間隙的嵌套的數據的能力; 2、算法是否需要預設條件:是否需要預先知道聚類個數,是否需要用戶給出領域知識;
3、算法的數據輸入屬性:算法處理的結果與數據輸入的順序是否相關,也就是說算法是否獨立於數據輸入順序;算法處理有很多屬性數據的能力,也就是對數據維數是否敏感,對數據的類型有無要求。
2.21.5 聚類和分類有什麽區別
聚類(Clustering) 聚類,簡單地說就是把相似的東西分到一組,聚類的時候,我們並不關心某一類是什麽,我們需要實現的目標只是把相似的東西聚到一起。一個聚類算法通常只需要知道如何計算相似度就可以開始工作了,因此聚類通常並不需要使用訓練數據進行學習,在機器學習中屬於無監督學習。
分類(Classification)
分類,對於一個分類器,通常需要你告訴它“這個東西被分為某某類”。一般情況下,一個分類器會從它得到的訓練集中進行學習,從而具備對未知數據進行分類的能力,在機器學習中屬於監督學習。
2.21.6 不同聚類算法特點性能比較
| 算法名稱 | 可伸縮性 | 適合的數據類型 | 高維性 | 異常數據抗幹擾性 | 聚類形狀 | 算法效率 |
|---|---|---|---|---|---|---|
| WAVECLUSTER | 很高 | 數值型 | 很高 | 較高 | 任意形狀 | 很高 |
| ROCK | 很高 | 混合型 | 很高 | 很高 | 任意形狀 | 一般 |
| BIRCH | 較高 | 數值型 | 較低 | 較低 | 球形 | 很高 |
| CURE | 較高 | 數值型 | 一般 | 很高 | 任意形狀 | 較高 |
| K-PROTOTYPES | 一般 | 混合型 | 較低 | 較低 | 任意形狀 | 一般 |
| DENCLUE | 較低 | 數值型 | 較高 | 一般 | 任意形狀 | 較高 |
| OPTIGRID | 一般 | 數值型 | 較高 | 一般 | 任意形狀 | 一般 |
| CLIQUE | 較高 | 數值型 | 較高 | 較高 | 任意形狀 | 較低 |
| DBSCAN | 一般 | 數值型 | 較低 | 較高 | 任意形狀 | 一般 |
| CLARANS | 較低 | 數值型 | 較低 | 較高 | 球形 | 較低 |
2.21.7 四種常用聚類方法之比較
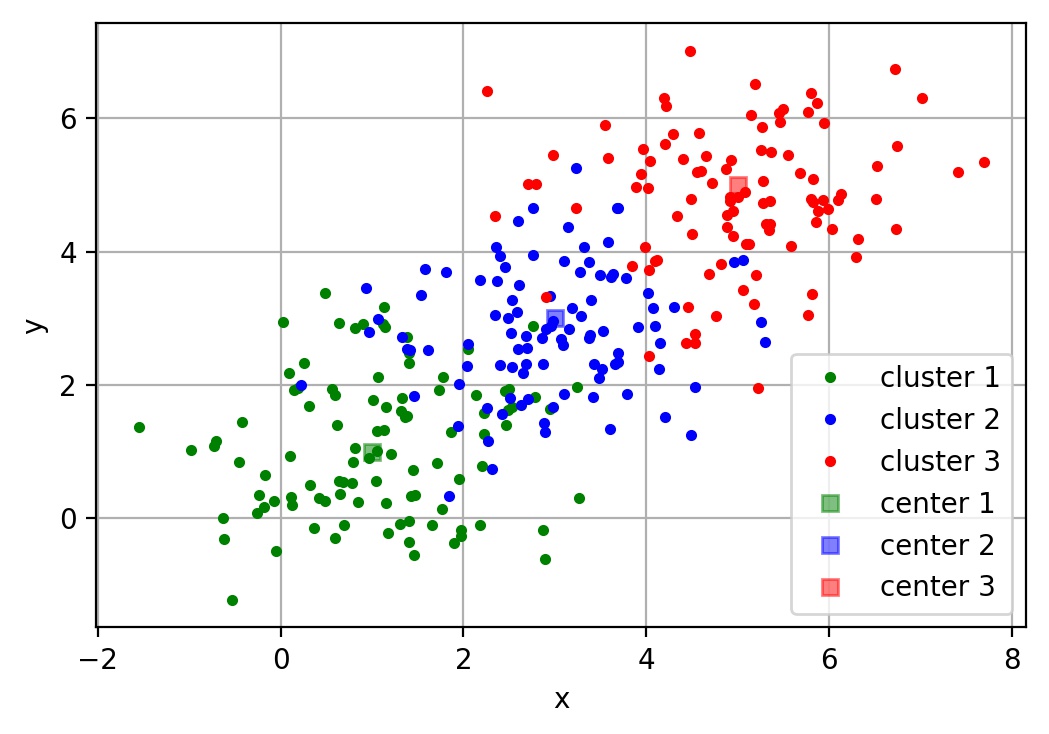
聚類就是按照某個特定標準把一個數據集分割成不同的類或簇,使得同一個簇內的數據對象的相似性盡可能大,同時不在同一個簇中的數據對象的差異性也盡可能地大。即聚類後同一類的數據盡可能聚集到一起,不同類數據盡量分離。 主要的聚類算法可以劃分為如下幾類:劃分方法、層次方法、基於密度的方法、基於網格的方法以及基於模型的方法。下面主要對k-means聚類算法、凝聚型層次聚類算法、神經網絡聚類算法之SOM,以及模糊聚類的FCM算法通過通用測試數據集進行聚類效果的比較和分析。
2.21.8 k-means聚類算法
k-means是劃分方法中較經典的聚類算法之一。由於該算法的效率高,所以在對大規模數據進行聚類時被廣泛應用。目前,許多算法均圍繞著該算法進行擴展和改進。 k-means算法以k為參數,把n個對象分成k個簇,使簇內具有較高的相似度,而簇間的相似度較低。k-means算法的處理過程如下:首先,隨機地 選擇k個對象,每個對象初始地代表了一個簇的平均值或中心;對剩余的每個對象,根據其與各簇中心的距離,將它賦給最近的簇;然後重新計算每個簇的平均值。 這個過程不斷重覆,直到準則函數收斂。通常,采用平方誤差準則,其定義如下: \(E=\sum_{i=1}^{k}\sum_{p\in C_i}\left\|p-m_i\right\|^2\) 這里E是數據中所有對象的平方誤差的總和,p是空間中的點,$m_i$是簇$C_i$的平均值[9]。該目標函數使生成的簇盡可能緊湊獨立,使用的距離度量是歐幾里得距離,當然也可以用其他距離度量。
算法流程: 輸入:包含n個對象的數據和簇的數目k; 輸出:n個對象到k個簇,使平方誤差準則最小。 步驟: (1) 任意選擇k個對象作為初始的簇中心; (2) 根據簇中對象的平均值,將每個對象(重新)賦予最類似的簇; (3) 更新簇的平均值,即計算每個簇中對象的平均值; (4) 重覆步驟(2)、(3)直到簇中心不再變化;
2.21.9 層次聚類算法
根據層次分解的順序是自底向上的還是自上向下的,層次聚類算法分為凝聚的層次聚類算法和分裂的層次聚類算法。 凝聚型層次聚類的策略是先將每個對象作為一個簇,然後合並這些原子簇為越來越大的簇,直到所有對象都在一個簇中,或者某個終結條件被滿足。絕大多數層次聚類屬於凝聚型層次聚類,它們只是在簇間相似度的定義上有所不同。
算法流程:
注:以采用最小距離的凝聚層次聚類算法為例:
(1) 將每個對象看作一類,計算兩兩之間的最小距離; (2) 將距離最小的兩個類合並成一個新類; (3) 重新計算新類與所有類之間的距離; (4) 重覆(2)、(3),直到所有類最後合並成一類。
2.21.10 SOM聚類算法
SOM神經網絡[11]是由芬蘭神經網絡專家Kohonen教授提出的,該算法假設在輸入對象中存在一些拓撲結構或順序,可以實現從輸入空間(n維)到輸出平面(2維)的降維映射,其映射具有拓撲特征保持性質,與實際的大腦處理有很強的理論聯系。
SOM網絡包含輸入層和輸出層。輸入層對應一個高維的輸入向量,輸出層由一系列組織在2維網格上的有序節點構成,輸入節點與輸出節點通過權重向量連接。 學習過程中,找到與之距離最短的輸出層單元,即獲勝單元,對其更新。同時,將鄰近區域的權值更新,使輸出節點保持輸入向量的拓撲特征。
算法流程:
(1) 網絡初始化,對輸出層每個節點權重賦初值; (2) 從輸入樣本中隨機選取輸入向量並且歸一化,找到與輸入向量距離最小的權重向量; (3) 定義獲勝單元,在獲勝單元的鄰近區域調整權重使其向輸入向量靠攏; (4) 提供新樣本、進行訓練; (5) 收縮鄰域半徑、減小學習率、重覆,直到小於允許值,輸出聚類結果。
2.21.11 FCM聚類算法
1965年美國加州大學柏克萊分校的紮德教授第一次提出了‘集合’的概念。經過十多年的发展,模糊集合理論漸漸被應用到各個實際應用方面。為克服非此即彼的分類缺點,出現了以模糊集合論為數學基礎的聚類分析。用模糊數學的方法進行聚類分析,就是模糊聚類分析[12]。
FCM算法是一種以隸屬度來確定每個數據點屬於某個聚類程度的算法。該聚類算法是傳統硬聚類算法的一種改進。
設數據集$X={x_1,x_2,…,x_n}$,它的模糊$c$劃分可用模糊矩陣$U=[u_{ij}]$表示,矩陣$U$的元素$u_{ij}$表示第$j(j=1,2,…,n)$個數據點屬於第$i(i=1,2,…,c)$類的隸屬度,$u_{ij}$滿足如下條件:
\(\begin{equation}
\left\{
\begin{array}{lr}
\sum_{i=1}^c u_{ij}=1 \quad\forall~j
\\u_{ij}\in[0,1] \quad\forall ~i,j
\\\sum_{j=1}^c u_{ij}>0 \quad\forall ~i
\end{array}
\right.
\end{equation}\)
目前被廣泛使用的聚類準則是取類內加權誤差平方和的極小值。即:
\((min)J_m(U,V)=\sum^n_{j=1}\sum^c_{i=1}u^m_{ij}d^2_{ij}(x_j,v_i)\)
其中$V$為聚類中心,$m$為加權指數,$d_{ij}(x_j,v_i)=||v_i-x_j||$。
算法流程:
(1) 標準化數據矩陣; (2) 建立模糊相似矩陣,初始化隸屬矩陣; (3) 算法開始叠代,直到目標函數收斂到極小值; (4) 根據叠代結果,由最後的隸屬矩陣確定數據所屬的類,顯示最後的聚類結果。
2.21.12 四種聚類算法試驗
選取專門用於測試分類、聚類算法的國際通用的UCI數據庫中的IRIS數據集,IRIS數據集包含150個樣本數據,分別取自三種不同 的鶯尾屬植物setosa、versicolor和virginica的花朵樣本,每個數據含有4個屬性,即萼片長度、萼片寬度、花瓣長度、花瓣寬度,單位為cm。 在數據集上執行不同的聚類算法,可以得到不同精度的聚類結果。基於前面描述的各算法原理及流程,可初步得如下聚類結果。
| 聚類方法 | 聚錯樣本數 | 運行時間/s | 平均準確率/(%) |
|---|---|---|---|
| K-means | 17 | 0.146001 | 89 |
| 層次聚類 | 51 | 0.128744 | 66 |
| SOM | 22 | 5.267283 | 86 |
| FCM | 12 | 0.470417 | 92 |
注:
(1) 聚錯樣本數:總的聚錯的樣本數,即各類中聚錯的樣本數的和;
(2) 運行時間:即聚類整個過程所耗費的時間,單位為s;
(3) 平均準確度:設原數據集有k個類,用$c_i$表示第i類,$n_i$為$c_i$中樣本的個數,$m_i$為聚類正確的個數,則$m_i/n_i$為 第i類中的精度,則平均精度為:$avg=\frac{1}{k}\sum_{i=1}^{k}\frac{m_{i}}{n_{i}}$。
參考文獻
[1] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.
[2] 周志華. 機器學習[M].清華大學出版社, 2016.
[3] Michael A. Nielsen. “Neural Networks and Deep Learning”, Determination Press, 2015.
[4] Suryansh S. Gradient Descent: All You Need to Know, 2018.
[5] 劉建平. 梯度下降小結,EM算法的推導, 2018
[6] 楊小兵.聚類分析中若幹關鍵技術的研究[D]. 杭州:浙江大學, 2005.
[7] XU Rui, Donald Wunsch 1 1. survey of clustering algorithm[J].IEEE.Transactions on Neural Networks, 2005, 16(3):645-67 8.
[8] YI Hong, SAM K. Learning assignment order of instances for the constrained k-means clustering algorithm[J].IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics,2009,39 (2):568-574.
[9] 賀玲, 吳玲達, 蔡益朝.數據挖掘中的聚類算法綜述[J].計算機應用研究, 2007, 24(1):10-13.
[10] 孫吉貴, 劉傑, 趙連宇.聚類算法研究[J].軟件學報, 2008, 19(1):48-61.
[11] 孔英會, 苑津莎, 張鐵峰等.基於數據流管理技術的配變負荷分類方法研究.中國國際供電會議, CICED2006.
[12] 馬曉艷, 唐雁.層次聚類算法研究[J].計算機科學, 2008, 34(7):34-36.
[13] FISHER R A. Iris Plants Database https://www.ics.uci.edu/vmlearn/MLRepository.html, Authorized license.
[14] Quinlan J R. Induction of decision trees[J]. Machine learning, 1986, 1(1): 81-106.
[15] Breiman L. Random forests[J]. Machine learning, 2001, 45(1): 5-32.


Comments